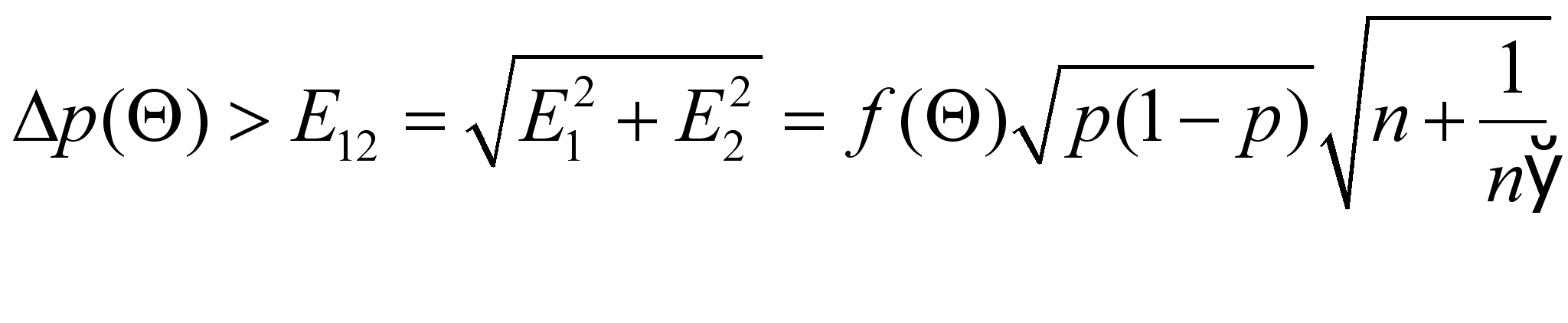Тема 3. Основы современных технологий диагностики качества знаний
3.1. Тестирование как метод контроля качества знаний
3.2. Компьютерное тестирование: возможности и особенности
3.3. Использование компьютерных тестирующих программ для проведения промежуточного и итогового контроля
3.4. Модели оценки результатов тестирования
3.4.1 Модели и методы проведения контроля
3.4.2 Надежность и валидность тестов
3.4.3 Практические методы оценки надежности тестов
3.4.4 Матричная алгебра в практической
работе с тестами
3.4.5 Точечные оценки
3.4. Модели оценки результатов тестирования
ТОЧЕЧНЫЕ
ОЦЕНКИ
Кроме коэффициента корреляции можно
использовать другие способы оценки выборки результатов. Из
результатов тестирования можно получить следующий ряд показателей:
математическое ожидание, дисперсию, среднеквадратическое отклонение,
размах вариации.
Точечной оценкой математического ожидания признака Х
является выборочное среднее[12].
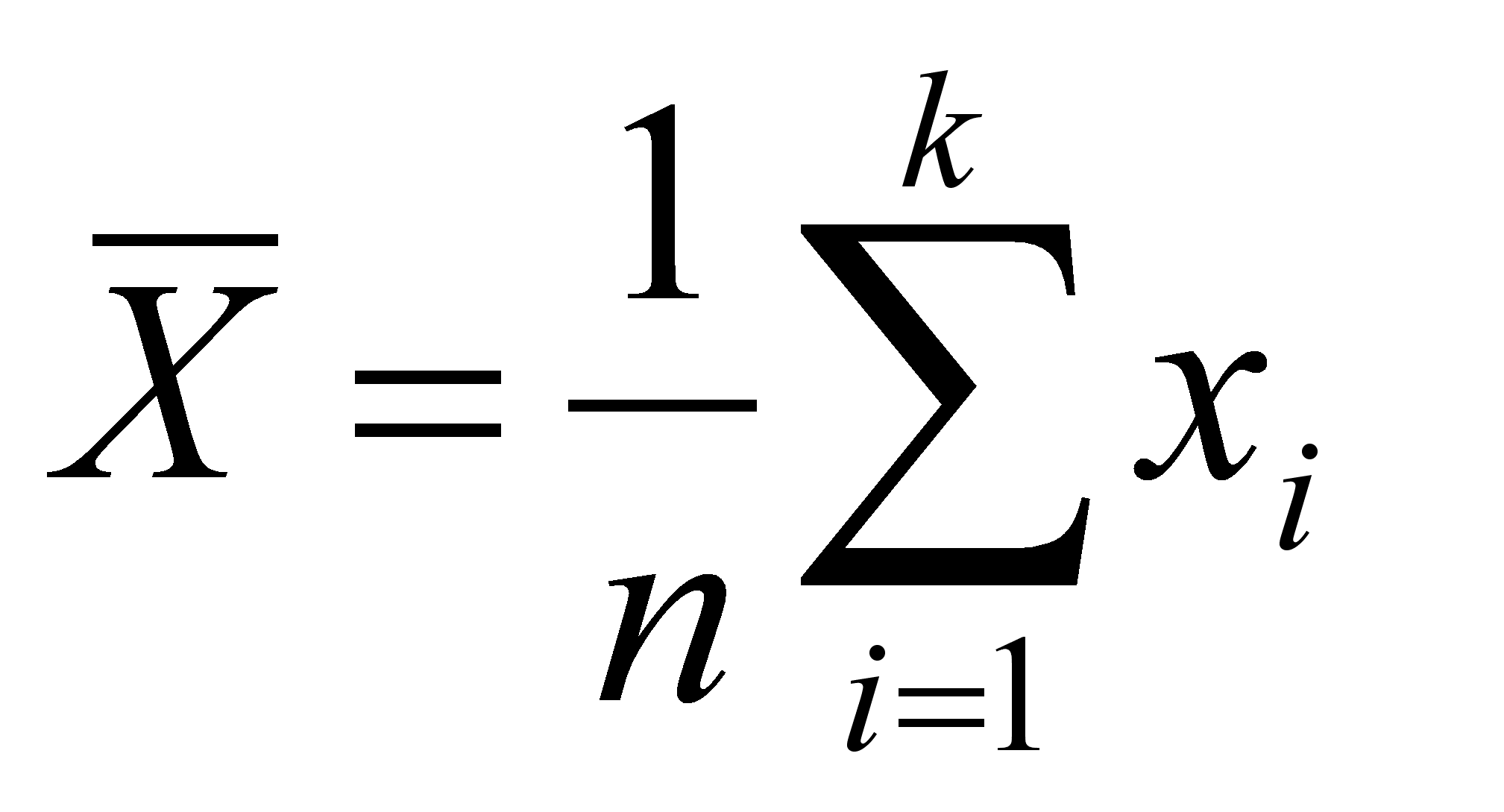
Д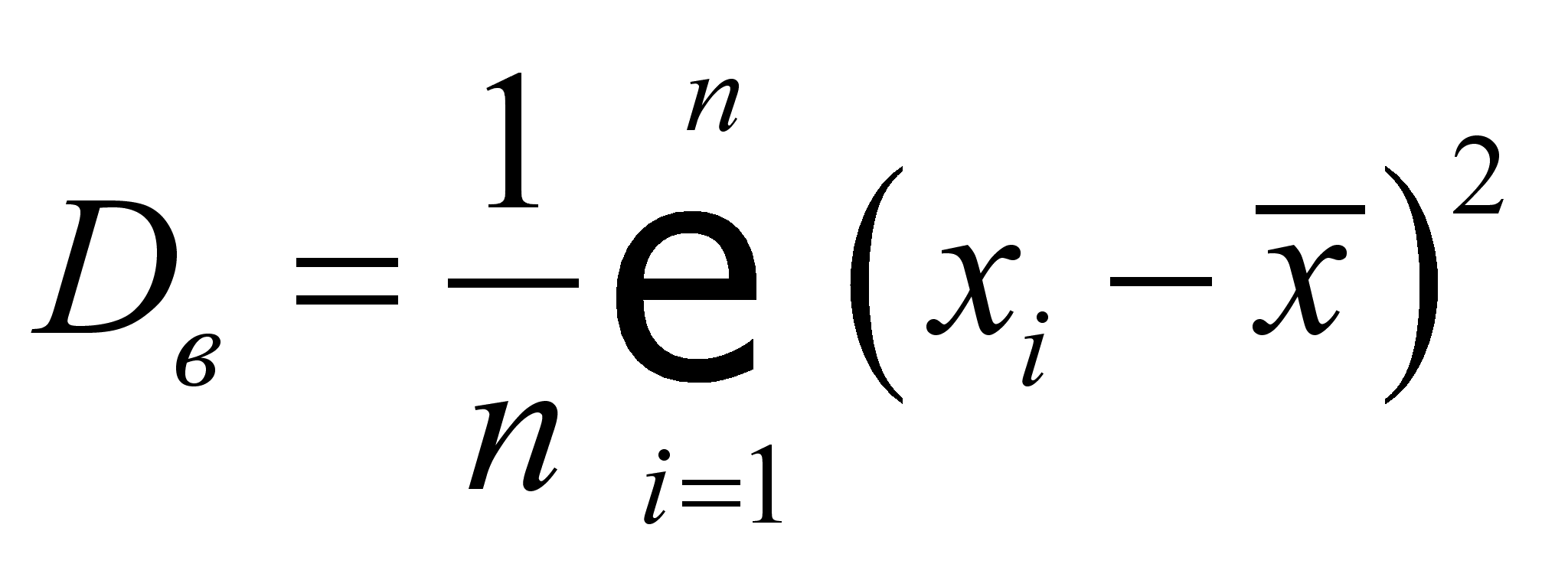 исперсия
является мерой рассеивания случайной величины около средней
арифметической. Чем больше дисперсия, тем больше величина разброса.
исперсия
является мерой рассеивания случайной величины около средней
арифметической. Чем больше дисперсия, тем больше величина разброса.
Среднеквадратическое отклонение служит для
характеристики рассеивания. Сравнение среднеквадратических отклонений
одного и того же признака в различных распределениях дает возможность
установить, где вариация признака больше.
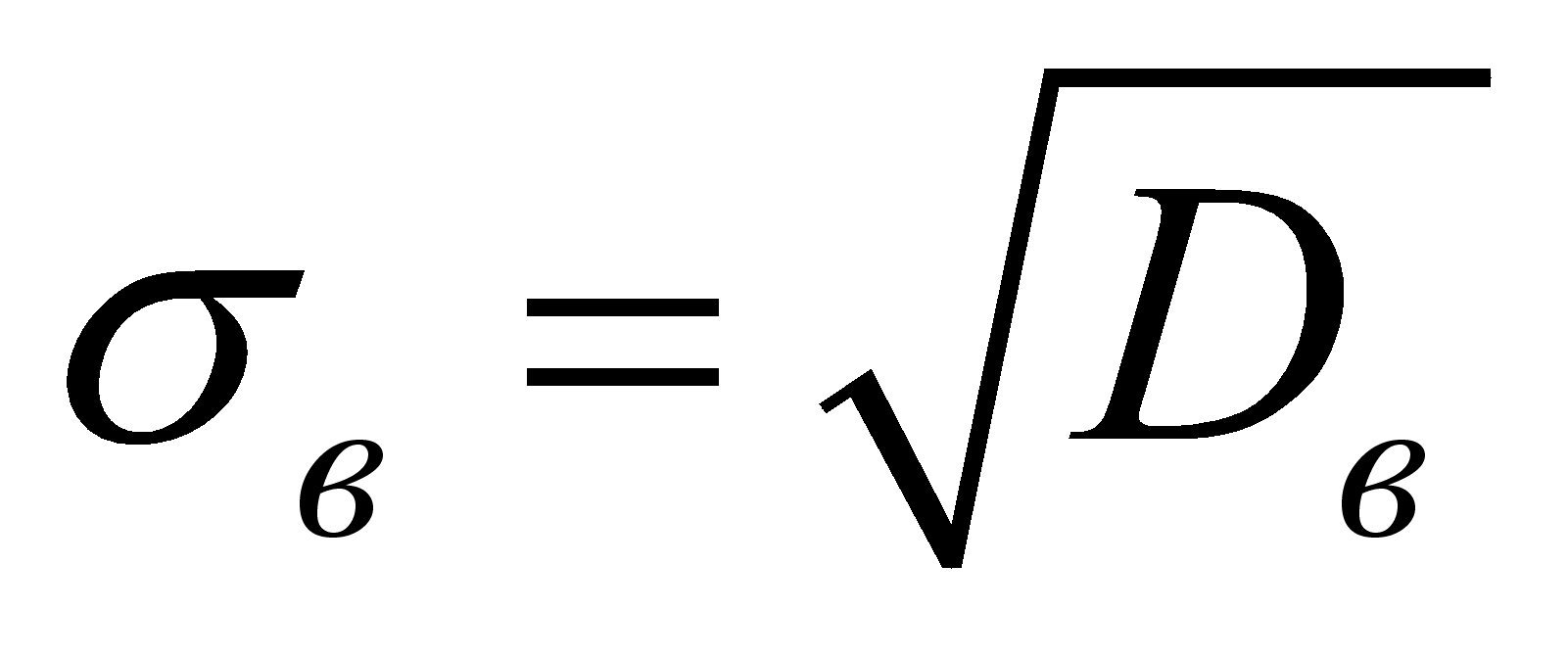
Размах вариации это разность между наибольшими и
наименьшими вариантами:
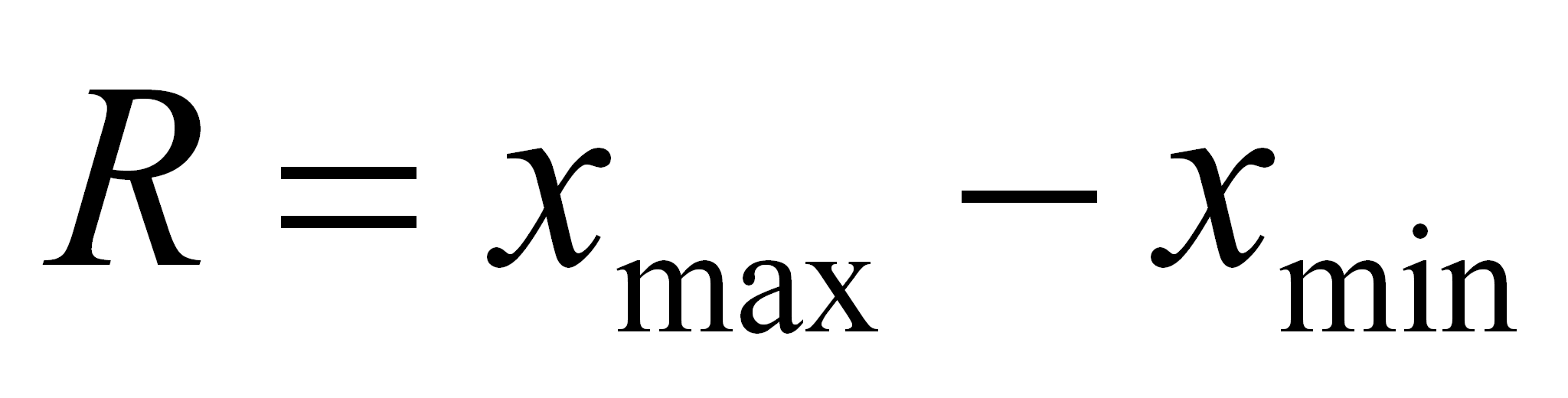
На размах вариации не влияют любые изменения
промежуточных значений признака, только бы эти значения не выходили
за крайние.
Результаты тестирования всегда можно представить
графически, тем более, что геометрическая иллюстрация статистических
данных придает им наглядность и позволяет подвергнуть их анализу в
наиболее простой и доступной форме. После получения результатов
тестирования, можно по имеющимся данным построить гистограмму
результатов. Но сама по себе гистограмма будет малоинформативной,
поэтому стоит сравнивать ее с оптимальным графиком нормального закона
распределения.

Рис.
2. Гистограмма тестовых результатов
Нормальное распределение – это распределение
частот, которые подчиняются закону нормального распределения. Именно
по этому закону в большинстве случаев распределяются результаты
выполнения тестов и их заданий.
Гистограмма – ступенчатая диаграмма. Для ее
построения на оси абсцисс откладывают значения признака и на каждом
из них, как на основании, строят прямоугольник с высотой, равной
соответствующей частоте[12].
Таким образом, в процессе отладки теста преподаватель
будет рассматривать результаты, полученные эмпирическим путем и
сравнивать их с теоретическими. Если он наблюдает большое отклонение
от нормы, он делает вывод о необходимости корректировки тестовых
заданий. Это, прежде всего, необходимо для отбора некорректно
составленных вопросов. В данном случае также имеет место использовать
комментарии, которые бы носили справочный характер и поясняли
отображаемые результаты.
Предполагается, что при проведении многочисленных
измерений результаты будут несколько отличаться друг от друга и
отклонения от среднего значения, полученного на большом числе
выборок, подчиняются закону нормального распределения.
Используя закон нормального распределения случайных
отклонений от среднего, можно оценить значение возможного случайного
отклонения при измерении уровня знаний на одной выборке из
 учащихся по формуле:
учащихся по формуле:
 ,
,
где
 - отношение числа правильных ответов ni
к общему числу ответов n, т.е. к
объему выборки:
- отношение числа правильных ответов ni
к общему числу ответов n, т.е. к
объему выборки:
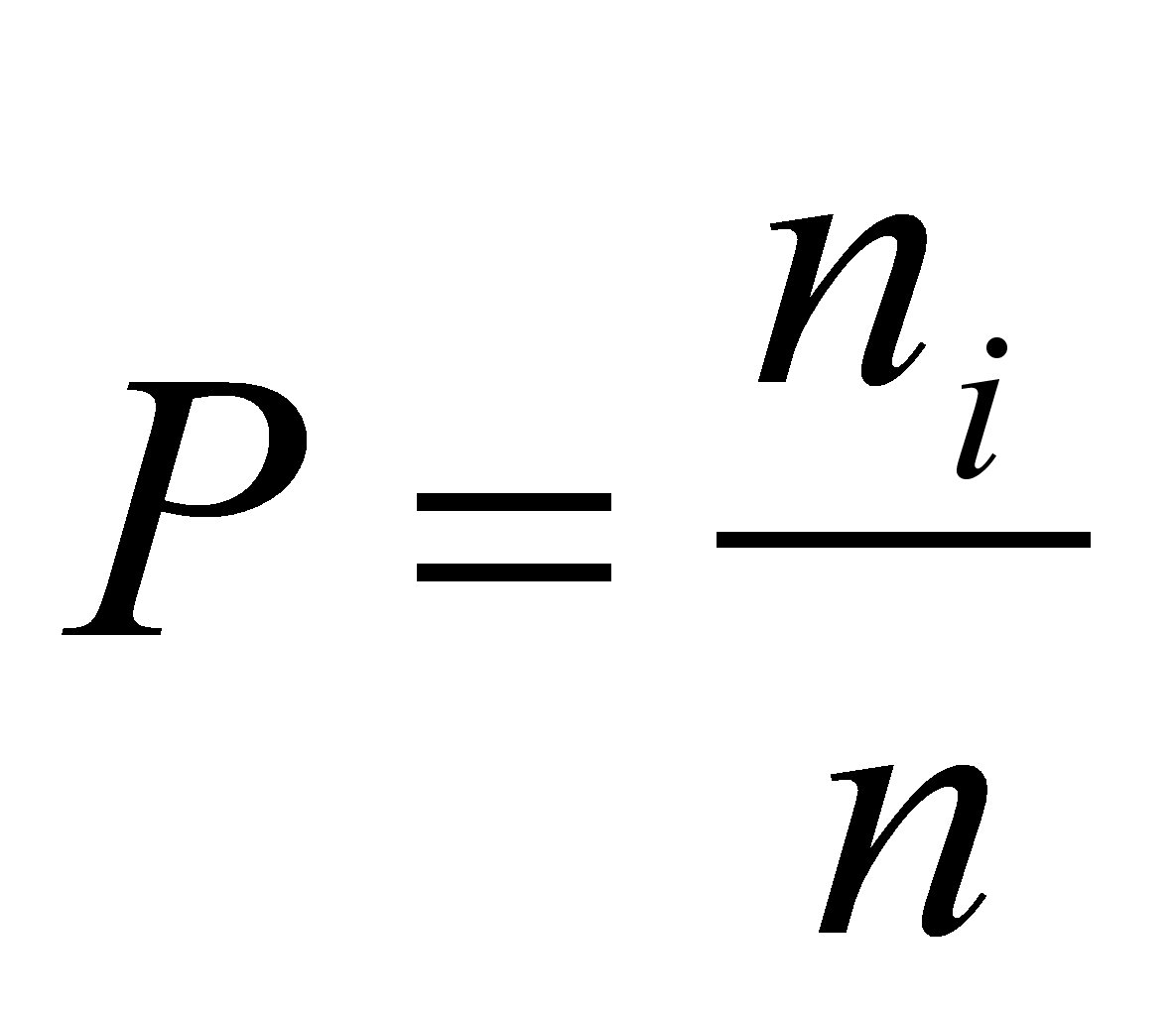 .
.
Коэффициент
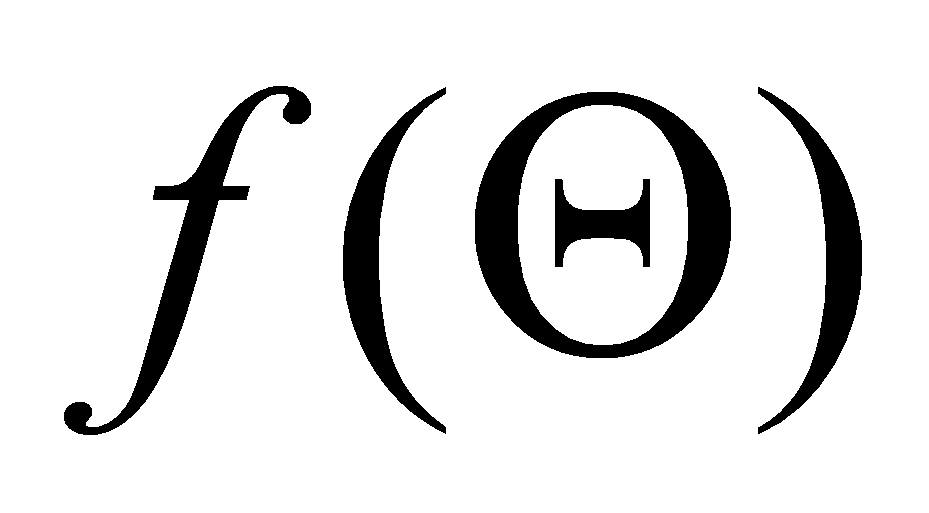 не
зависит ни от объема выборки, ни от частоты P
правильных ответов, а полностью определяется выбором уровня
достоверности Θ. Значения
не
зависит ни от объема выборки, ни от частоты P
правильных ответов, а полностью определяется выбором уровня
достоверности Θ. Значения
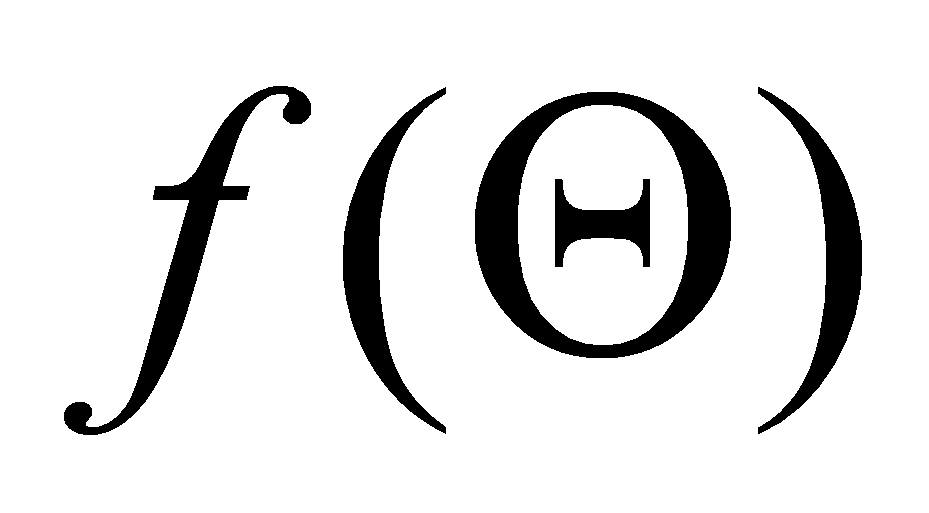 выводятся
из закона нормального распределения и задаются обычно таблицами. Для
тестов рекомендуется выбирать уровень достоверности Θ = 0,90.
выводятся
из закона нормального распределения и задаются обычно таблицами. Для
тестов рекомендуется выбирать уровень достоверности Θ = 0,90.
Смысл вычисляемой по указанной выше формуле нормальной
погрешности E(Θ) заключается в
следующем. При одинаковых принципах формирования выборок и условиях
обучения частота pi
правильных ответов на i-е задание
теста в выборке из n учащихся отличается от
частоты pi правильных
ответов на то же задание в выборке объема N
(N>>n)
не более чем на величину E(Θ),
с достоверностью Θ, т.е. в Θ% случаев.
При отличии частоты pi
правильных ответов в выборке объема n
от частоты pi правильных
ответов в выборке большего объема N
на величину, превышающую значение нормальной погрешности E(Θ),
с достоверность можно утверждать, что это отличие не случайное.
Если при идентичных измерениях в двух выборках получены
значения p и p’
(доли правильных ответов на i-й
вопрос), то при сравнении результатов необходимо учитывать
погрешности обоих измерений. Различие между p
и p’ может оказаться незначимым на
каком-то уровне достоверности, т.е. объяснимым только случайными
ошибками.
В случае нормального распределения погрешностей
измерений различие между p и p’
является значимым на уровне достоверности Θ, если разность p
- p’ превышает значение
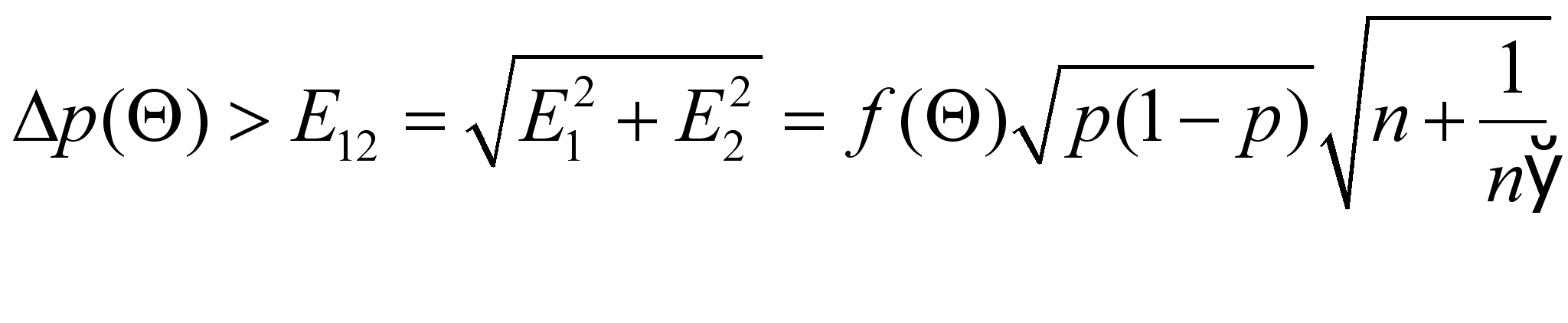
где n и n’
– объемы выборок,
p – средняя доля
правильных ответов в совокупности этих выборок[14].
Из этого следует, что по результатам сравнения
нескольких выборок тестирования, можно делать вывод о том, что в
контрольном задании, возможно, присутствуют некорректно составленные
вопросы.
Не маловажное значение при тестировании имеет
возможность предсказать результаты. Под этим подразумевается то, что
после проведения нескольких этапов отладки теста преподаватель должен
знать, что в группе испытуемых, аналогичной предыдущим по своей
подготовке, он получит приблизительно такой же результат. Гипотезы о
распределении тестовых выборок можно проверять, использую различные
статистические критерии.

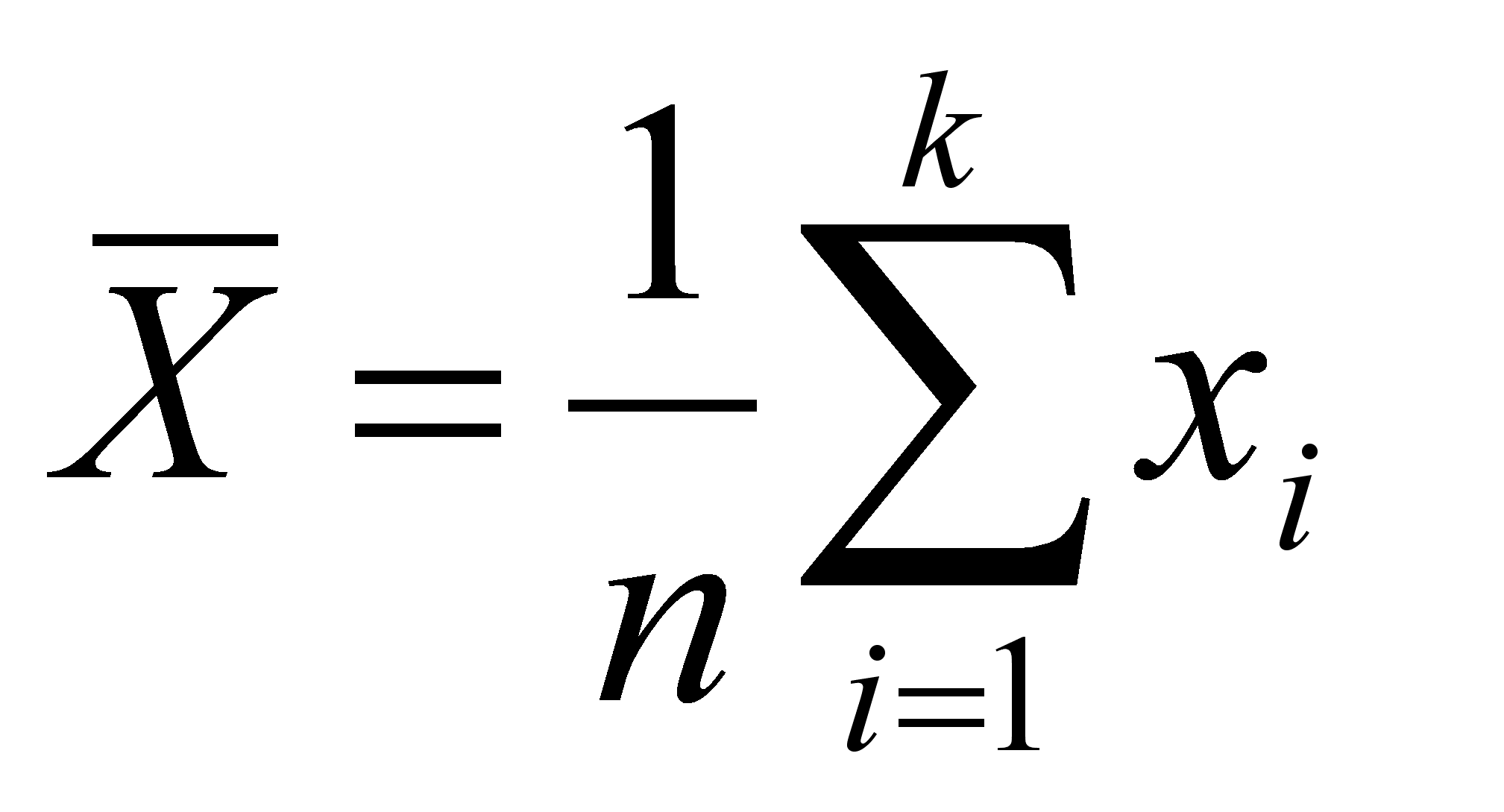
![]() исперсия
является мерой рассеивания случайной величины около средней
арифметической. Чем больше дисперсия, тем больше величина разброса.
исперсия
является мерой рассеивания случайной величины около средней
арифметической. Чем больше дисперсия, тем больше величина разброса.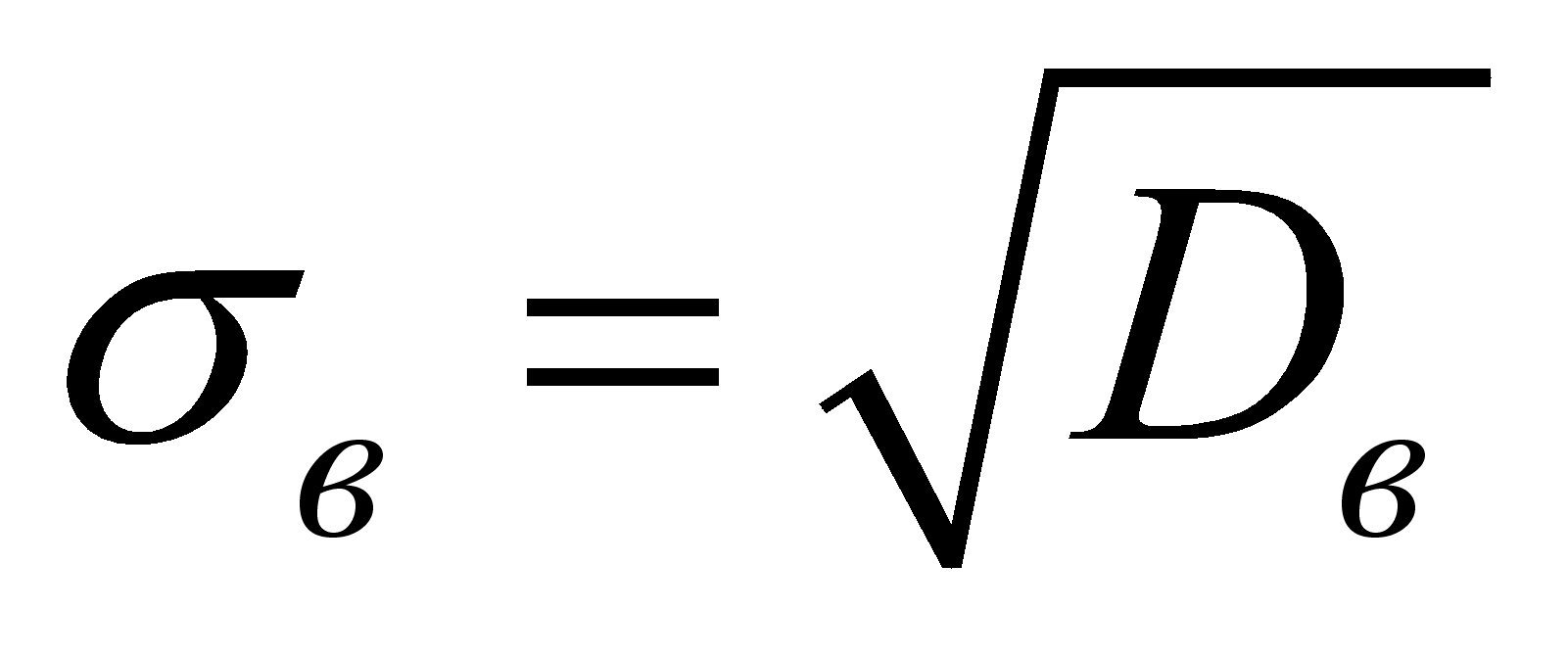
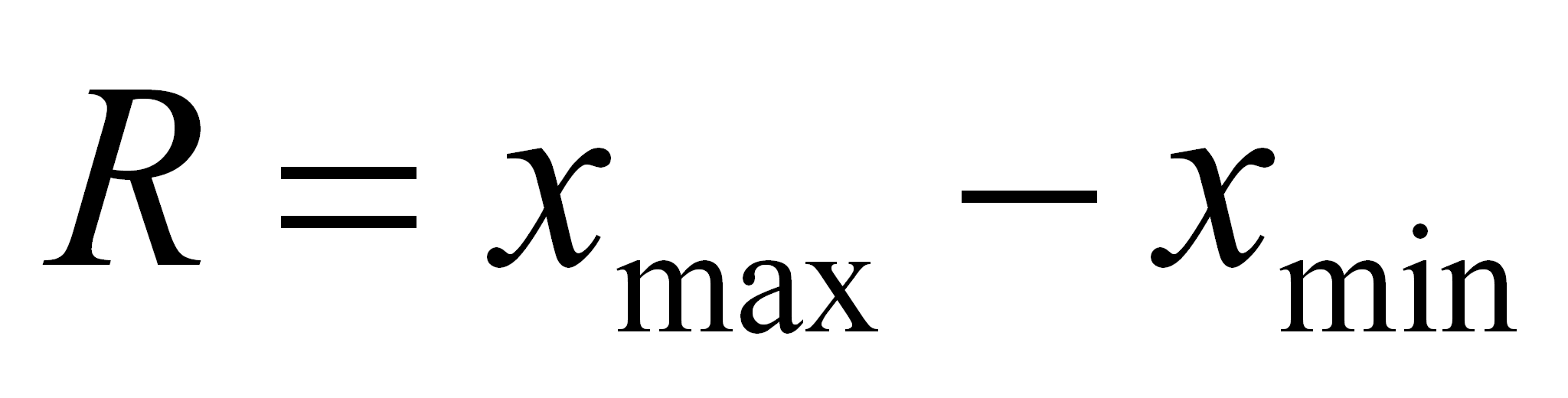

 ,
, - отношение числа правильных ответов
- отношение числа правильных ответов 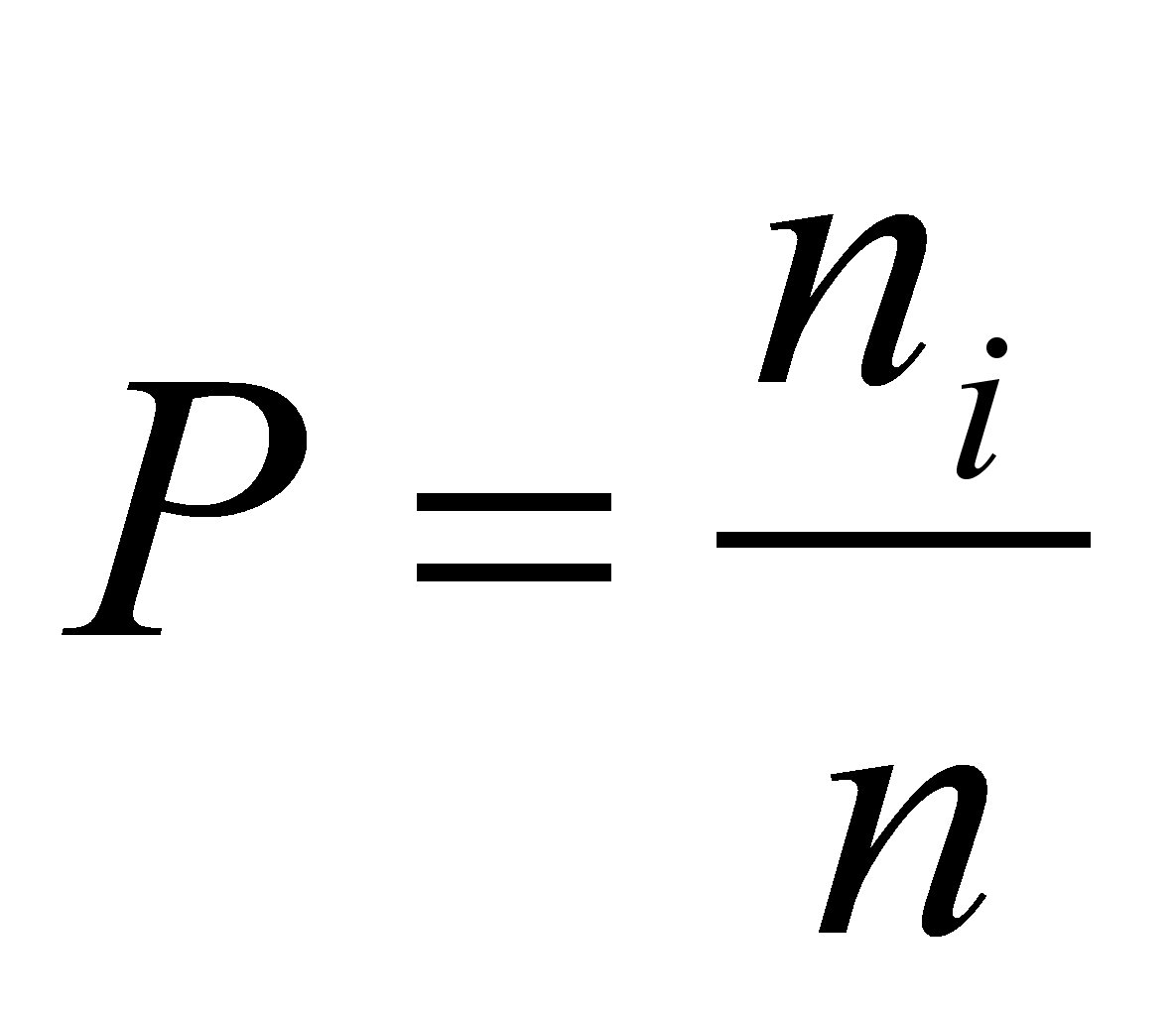 .
.