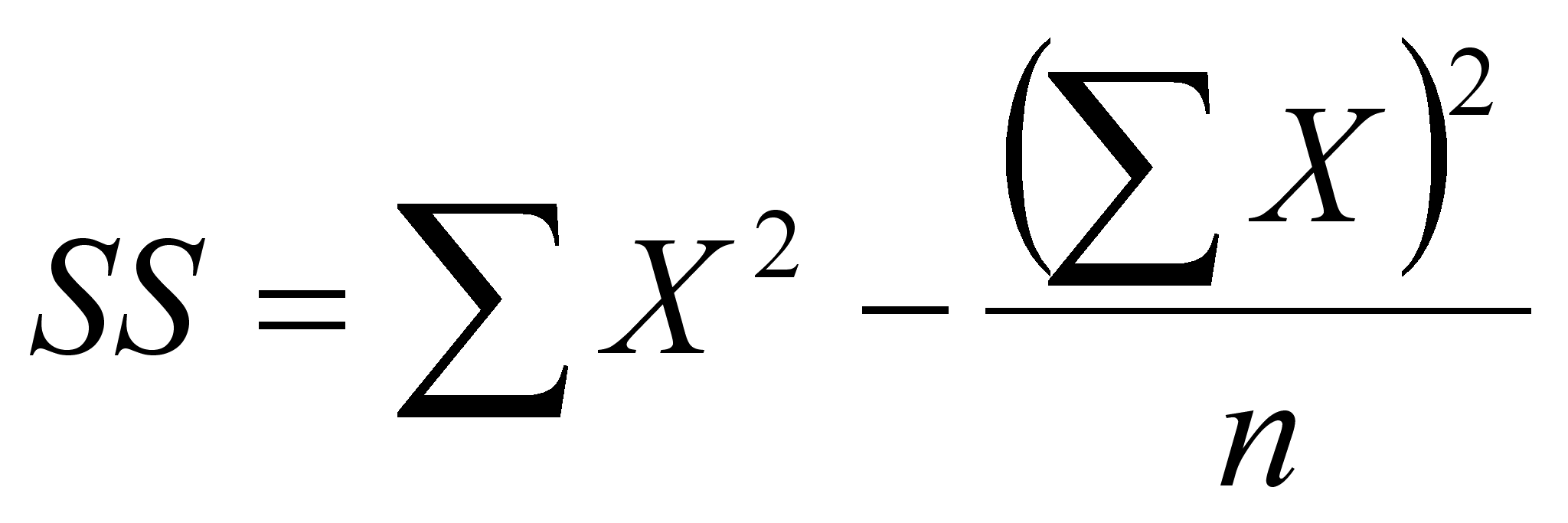
Тема 3. Основы современных технологий диагностики качества знаний
В.С.Аванесов предлагает анализировать результаты теста, используя коэффициент корреляции.
Коэффициент корреляции - числовая характеристика совместного распределения двух случайных величин, выражающая их взаимосвязь. Если коэффициент больше 0, то при увеличении значений одной из величин, вторая имеет тенденцию к увеличению; если меньше нуля – к снижению.
Для расчета коэффициента корреляции используются последовательно четыре формулы:
Вначале находится сумма квадратов отклонений баллов испытуемых от среднего арифметического балла в интересующем задании. Это делается по формуле:
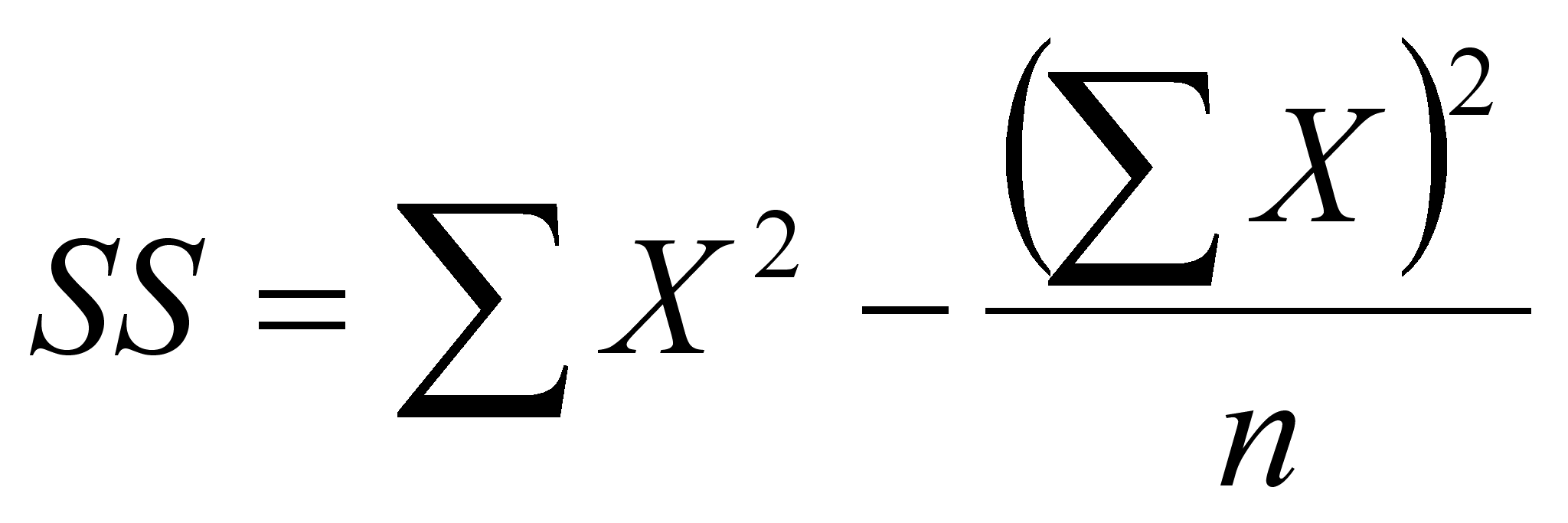
Затем находится сумма квадратов отклонений тестовых баллов испытуемых от среднего арифметического балла по всему тесту.
Находится скорректированная на средние значения сумма попарных произведений X и Y, по формуле:
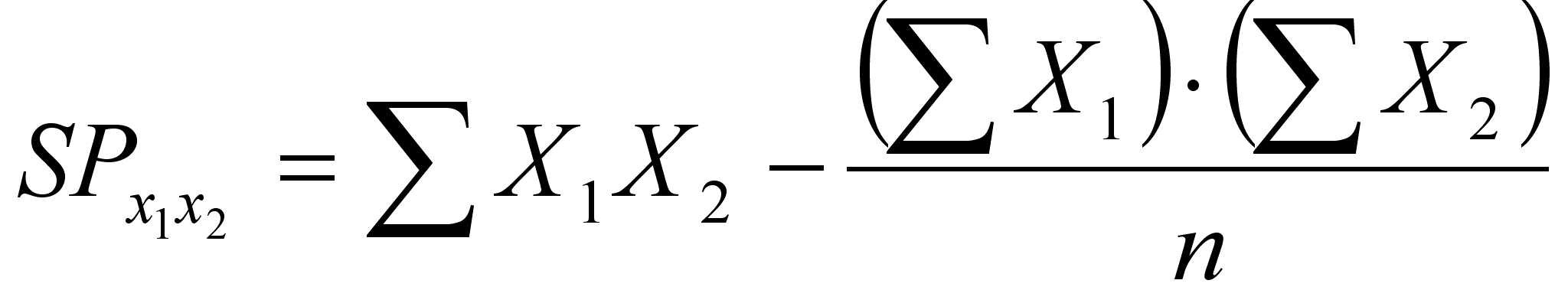
В этой формуле
![]() представляет
собой сумму произведений баллов каждого испытуемого по i-му
заданию и по i-му тестовому баллу
испытуемых. Вторая часть формулы представляет собой коррекцию на
средние значения X1 и X2.
представляет
собой сумму произведений баллов каждого испытуемого по i-му
заданию и по i-му тестовому баллу
испытуемых. Вторая часть формулы представляет собой коррекцию на
средние значения X1 и X2.
Рассчитывается коэффициент корреляции по формуле:
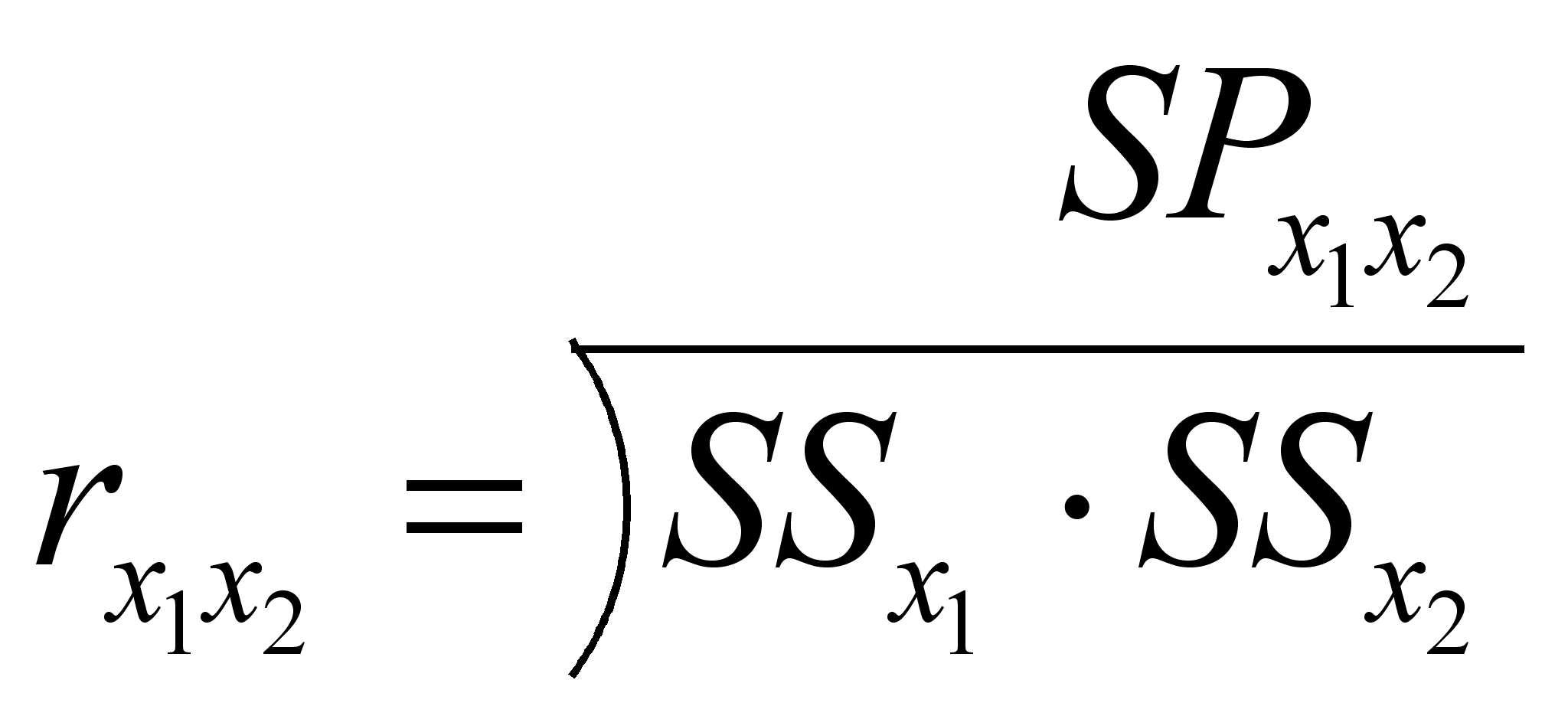
Рассмотрим анализ результатов тестирования на конкретном примере. Для удобства оперирования большими массивами чисел используется специальный аппарат матричной алгебры. Предположим, что шесть респондентов (n=6) ответили на три высказывания теста (k=3). Если за ответ, совпадающий с ключом, давать респонденту один балл, а за прочие ответы – ноль, то результаты такого опроса можно представить в виде матрицы чисел. Обозначим ее буквой А.
А
=

-----------------------
![]()
![]()
В тесте, где оценки даются по семибалльной шкале, результаты у шести опрошенных в трёх утверждениях представим следующим образом:
В
=
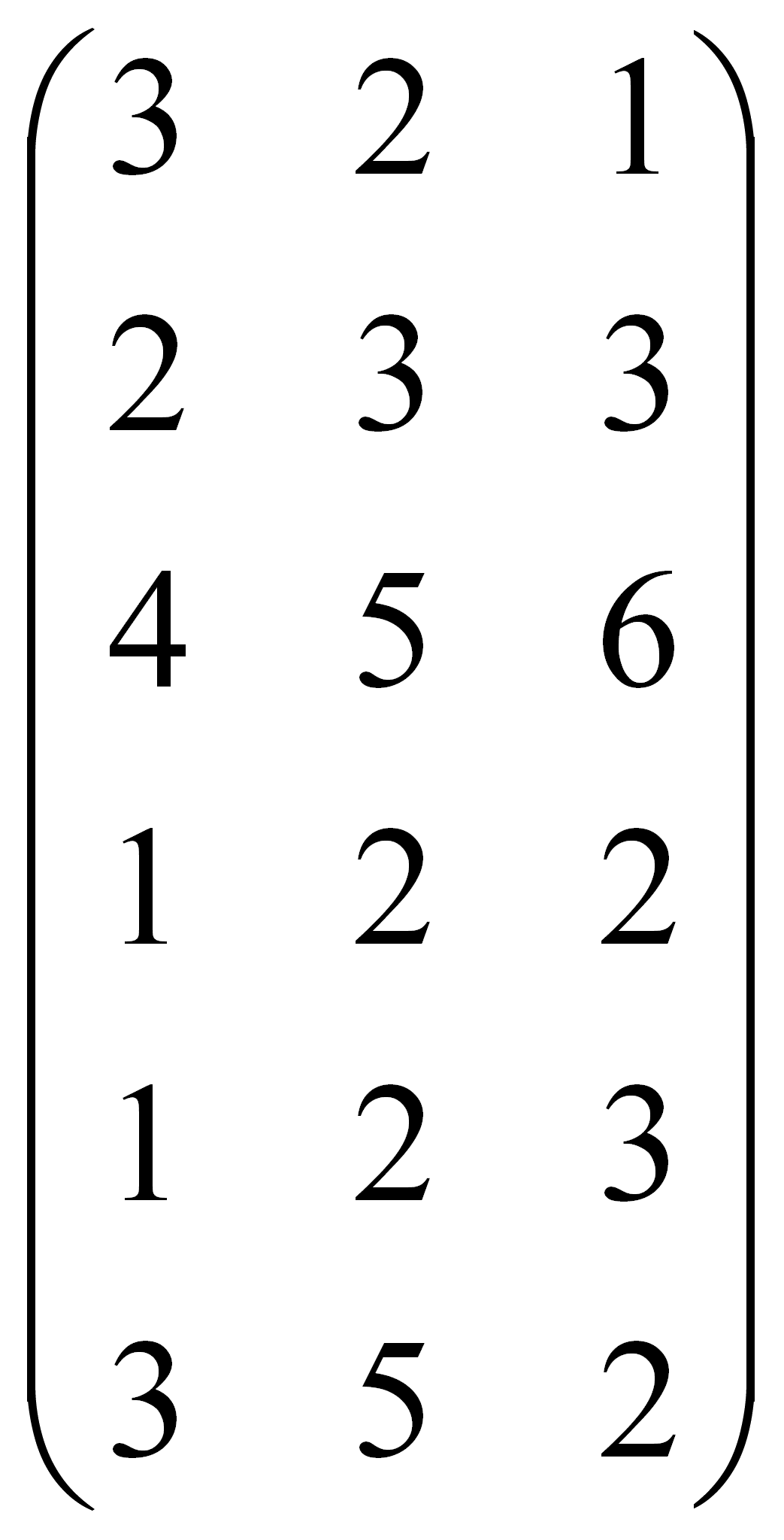
----------------------
![]()
![]()
После проведения тестирования мы можем получить следующие результаты: сложив элементы матрицы по столбцам, получаем сумму баллов, набранную респондентами в каждом отдельном высказывании. Анализ полученных сумм показывает, что в результате первого тестирования больше баллов получено в третьем высказывании, меньше – в первом. Аналогично результаты второго теста показывают, что во втором задании сумма балов за ответы наибольшая, в первом – наименьшая.
Средние арифметические значения находятся по формуле
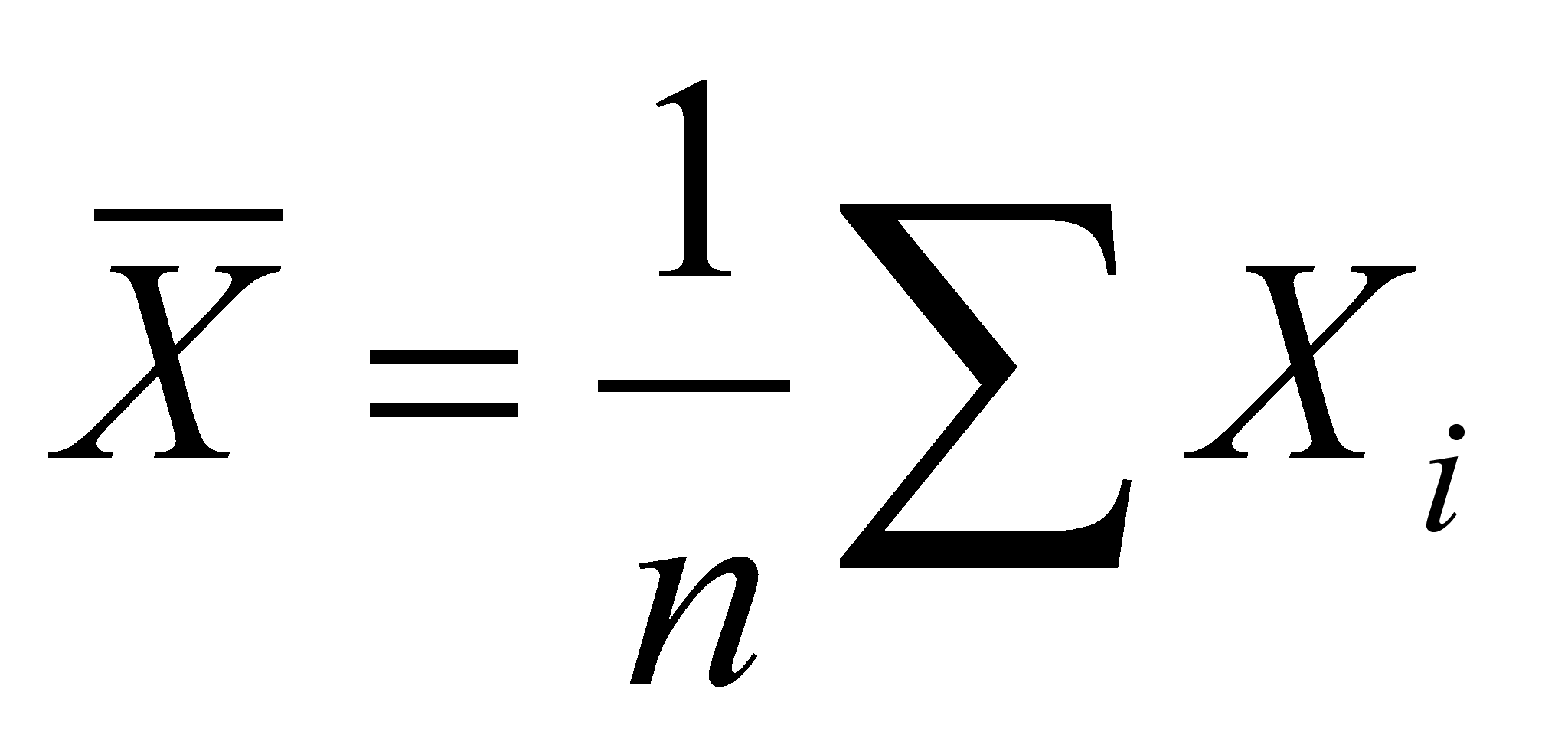
где
![]() - средняя арифметическая,
- средняя арифметическая,
n – число респондентов,
Xi – балл респондента i в отдельном высказывании.
Если в каждом столбце А или В отнять соответствующие им средние арифметические значения, то получим отклонение от средней арифметической.

Произведение Х на Х’ дает матрицу SPSS:
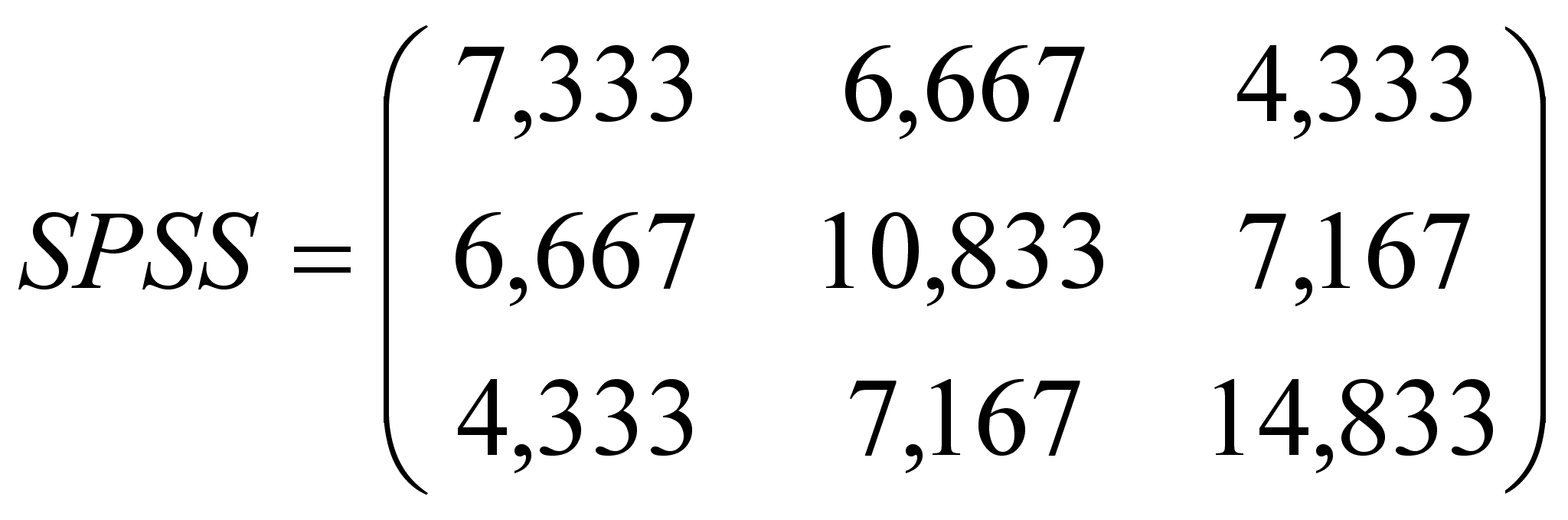 .
.
Матрица SPSS примечательна
тем, что элементы ее главной диагонали
![]() есть суммы квадратов отклонений от средних арифметических (SS).
Внедиагональные элементы этой матрицы образуют величины, необходимые
для расчеты коэффициентов корреляции. Существует и другой способ
получения этих значений. Формула расчёта SS:
есть суммы квадратов отклонений от средних арифметических (SS).
Внедиагональные элементы этой матрицы образуют величины, необходимые
для расчеты коэффициентов корреляции. Существует и другой способ
получения этих значений. Формула расчёта SS:
![]() .
.
Существует эквивалентная ей формула:
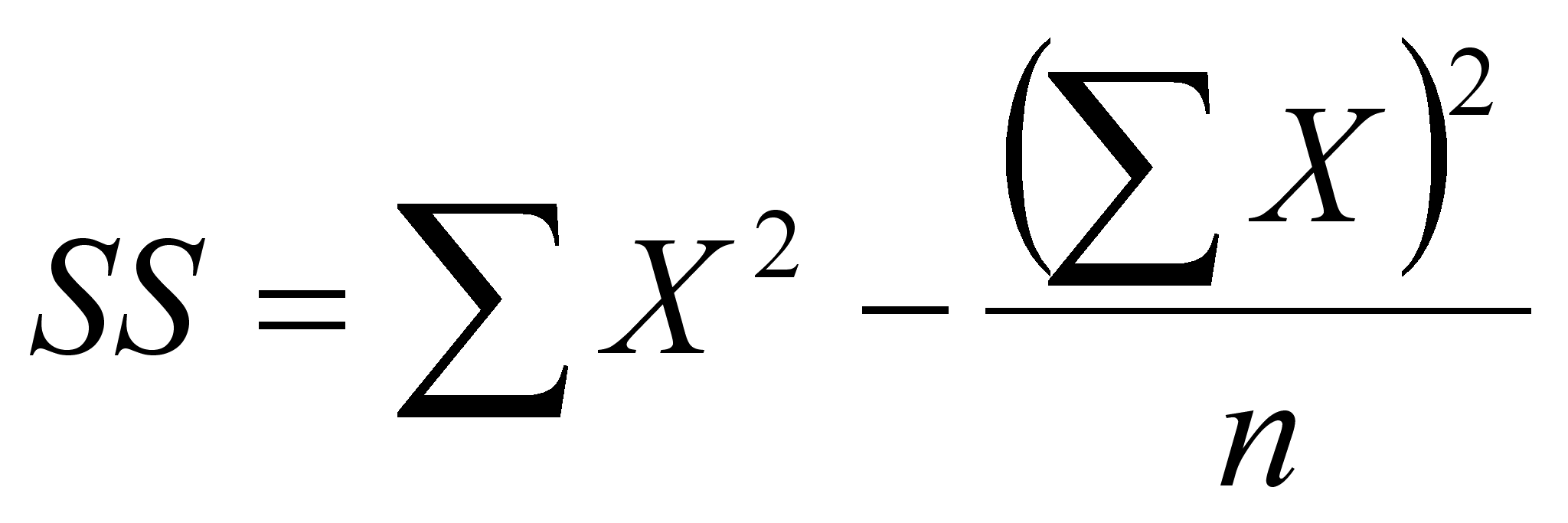 .
.
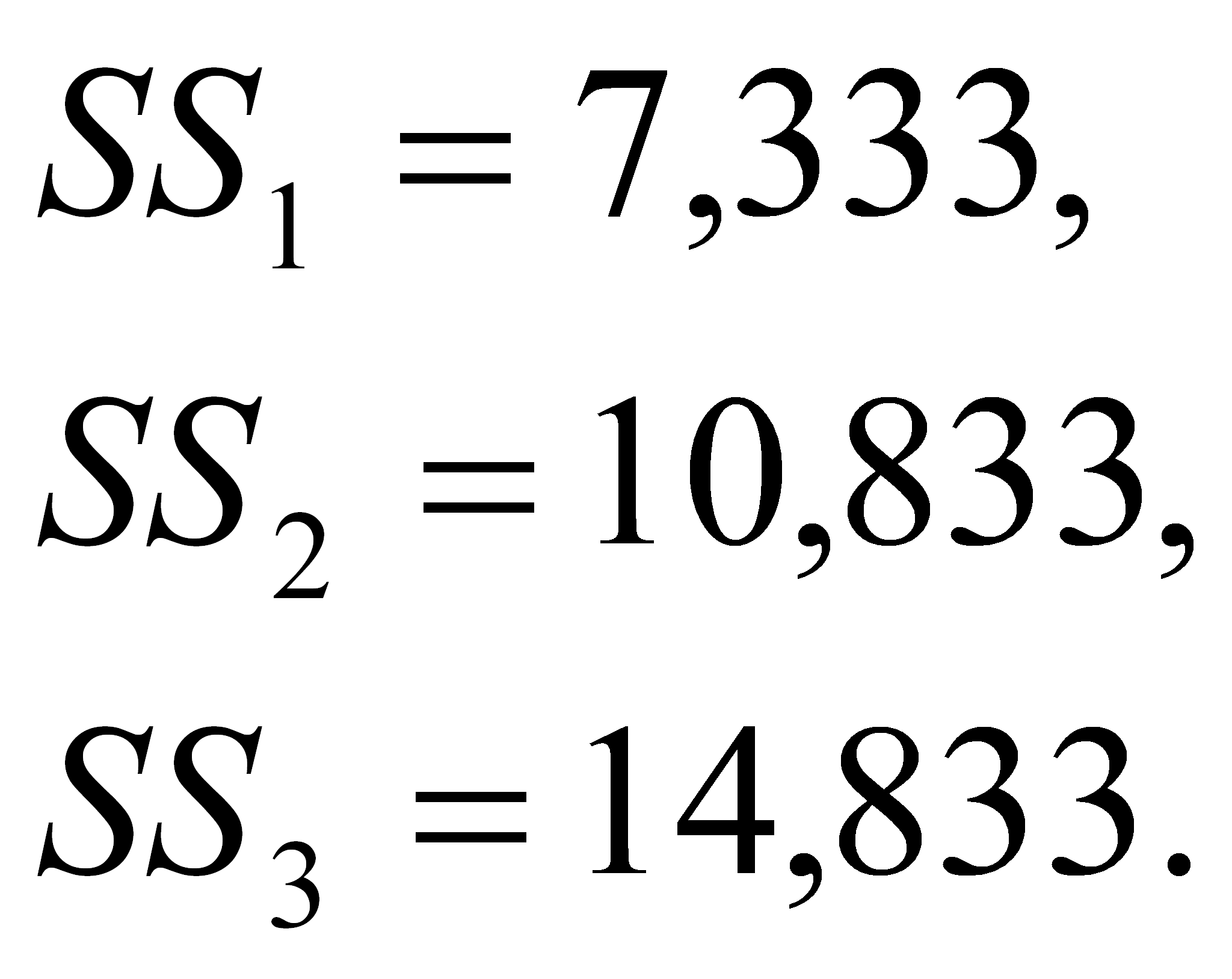
Формула расчета значений ![]() - скорректированных сумм произведений элементов X1
на X2:
- скорректированных сумм произведений элементов X1
на X2:
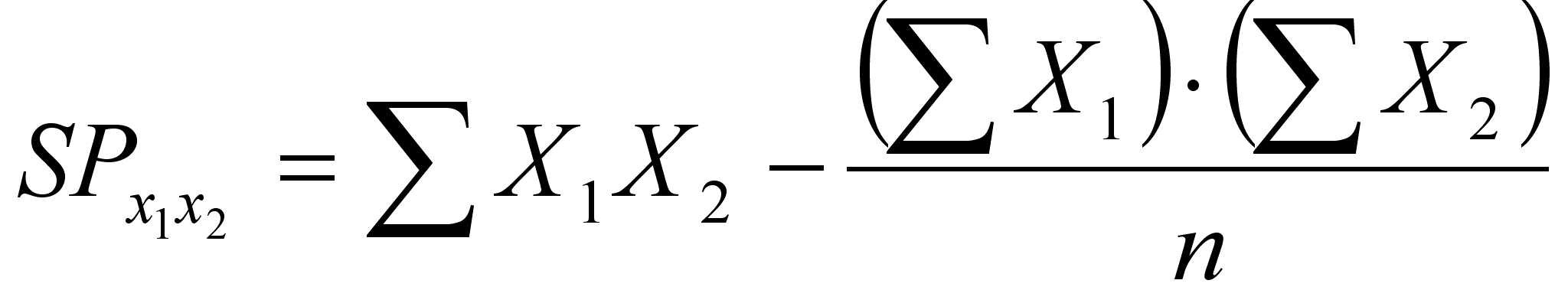 .
.
Расчеты SP и SS сводятся в матрицу SPSS.
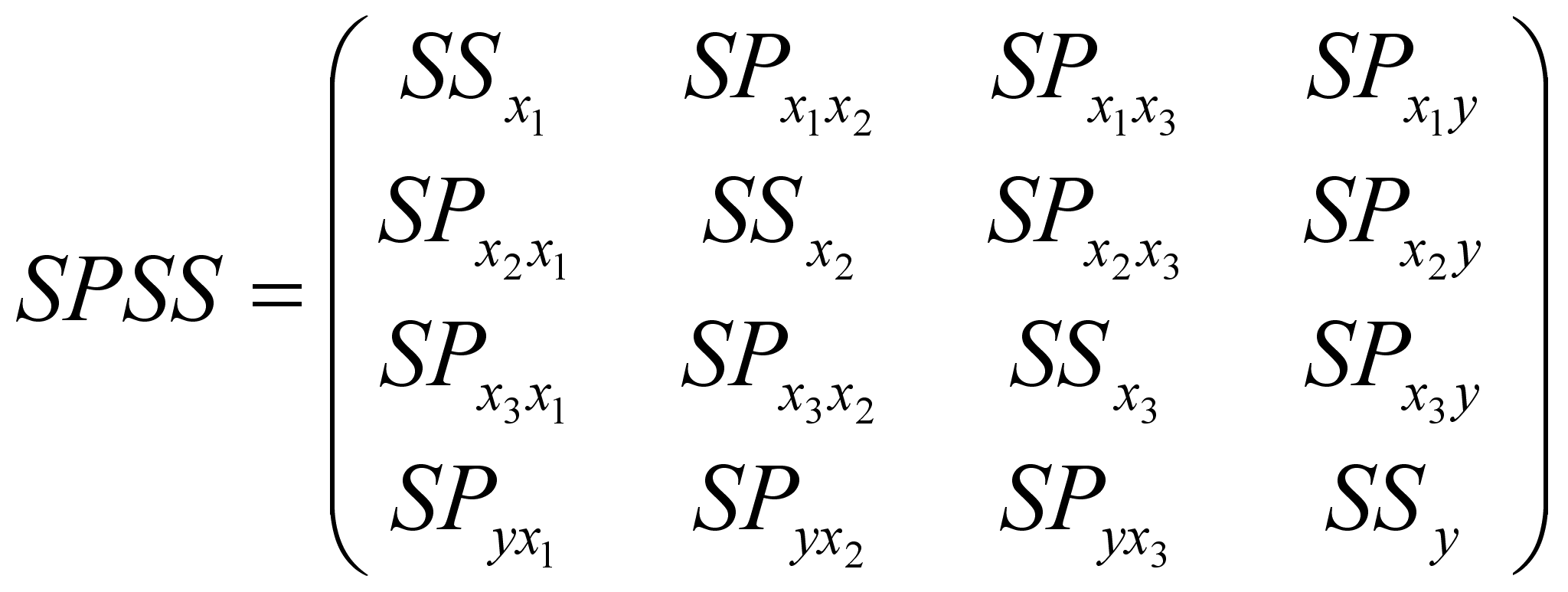 .
.
После расчетов матрица SPSS для матрицы В примет следующий вид:
 .
.
Сравнивая матрицу SPSS, ранее полученную как результат матричного умножения X’X и матрицу SPSS, рассчитанную по указанным формулам, мы можем видеть полное совпадение результатов, если не считать добавленного в последнем случае вектора Y.
Полученные значения позволяют сразу же перейти к расчёту главных характеристик как теста в целом, так и отдельных его высказываний.
Дисперсия S2 рассчитывается по формуле
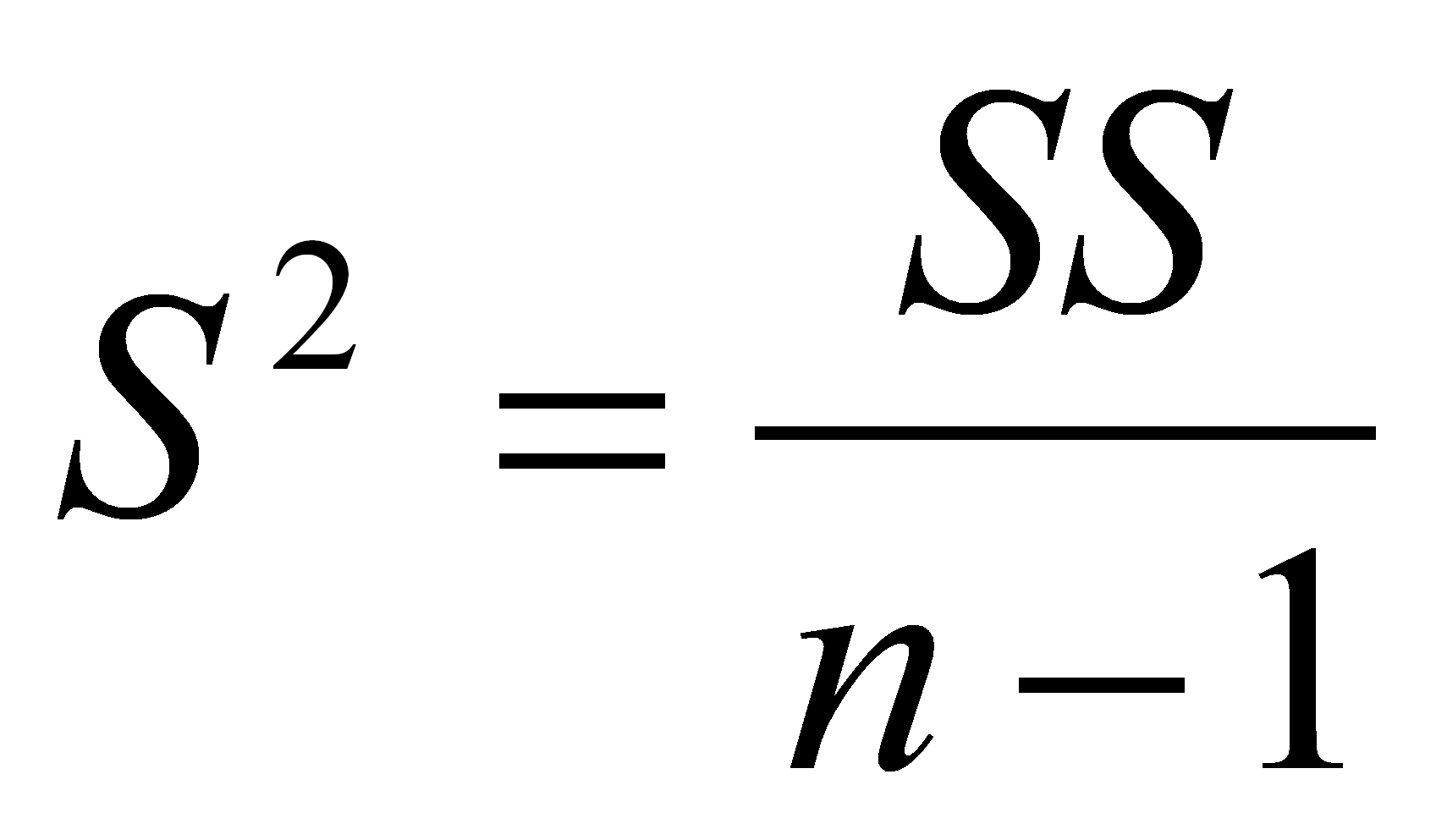 ,
,
а стандартное отклонение S:
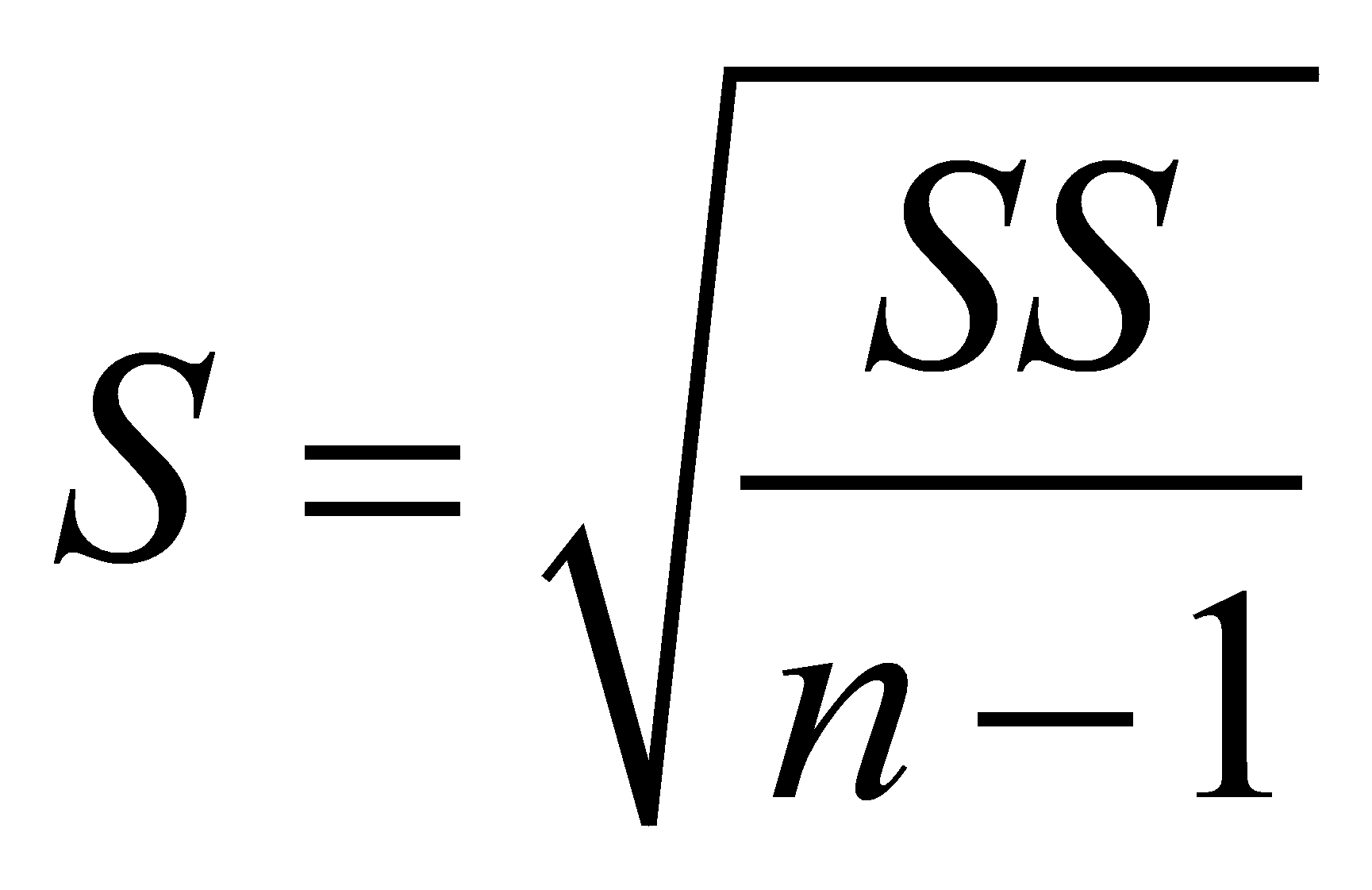 .
.
Все произведенные расчеты полезно свести в одну матрицу. Для этого расширим исходные матрицы А и В, включив в них суммарные векторы.
В тестовой практике часты случаи, когда наличие
интересующего признака оценивается единицей, отсутствие –
нулем. Примером таких данных является матрица А. Вначале
рассчитывается доля правильных ответов, указывающих на наличие
признака – p. Для случая
дихотомических данных
![]() .
Находим
далее
.
Находим
далее
![]() .
Произведение
.
Произведение
![]() дает
сумму квадратов отклонений от средних арифметических (SS).
дает
сумму квадратов отклонений от средних арифметических (SS).
Деление SP и SS на n-1 дает значение ковариаций и дисперсий. Извлекая корень из дисперсии, получим стандартное отклонение каждого утверждения теста и суммарных векторов Y. Для того, чтоб рассчитать коэффициенты корреляции необходимо воспользоваться формулой
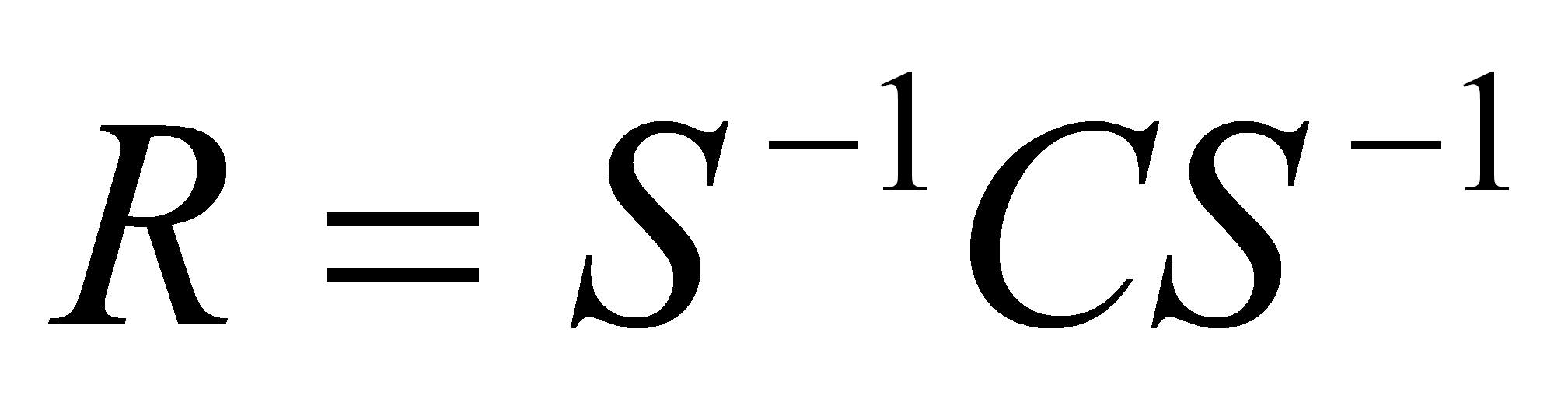 .
.
Иначе коэффициент корреляции можно получить
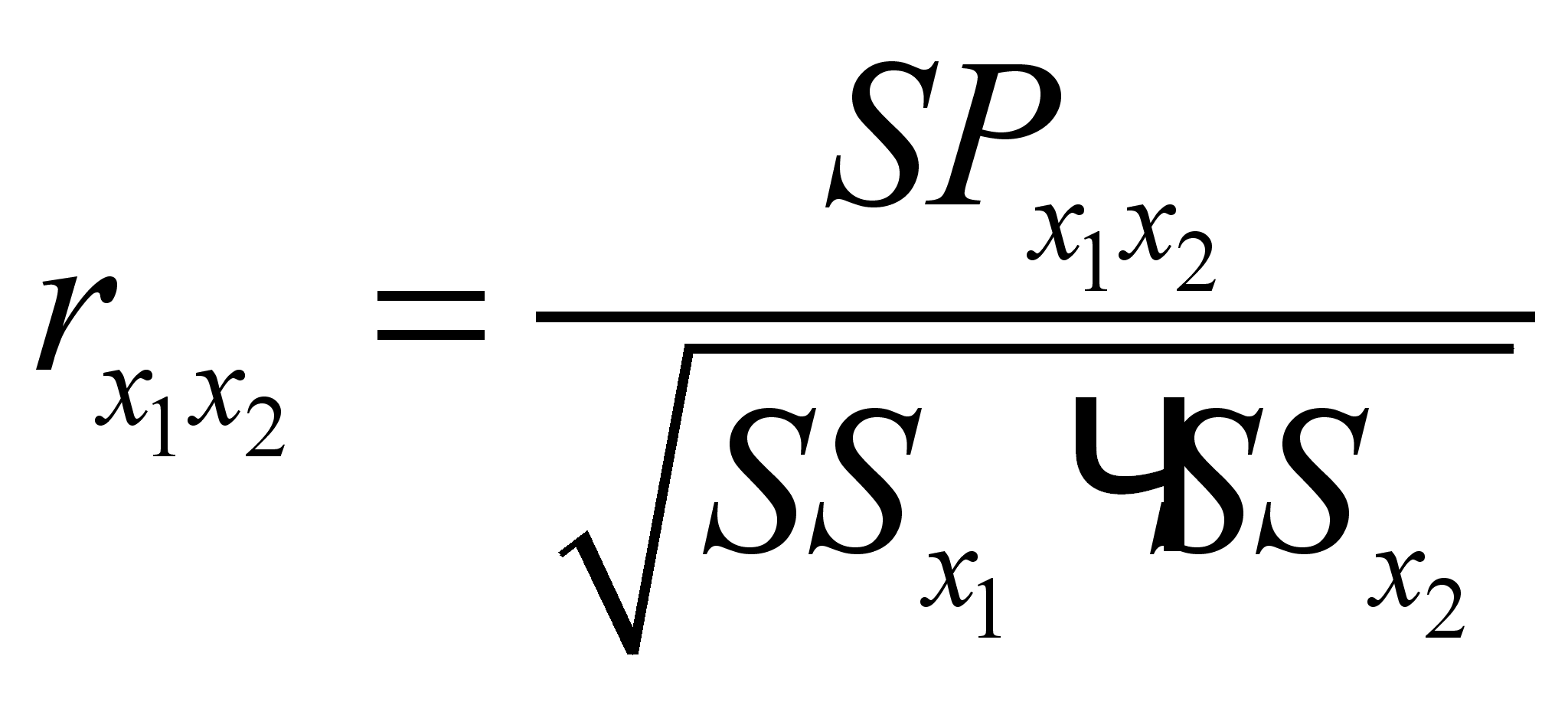 ,
,
где
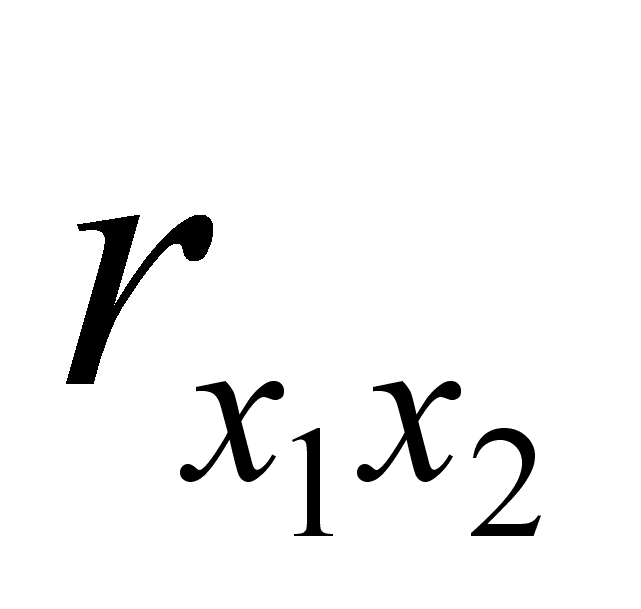 -
коэффициент корреляции первого утверждения со вторым.
-
коэффициент корреляции первого утверждения со вторым.
Таблица 2 показывает как мы можно оценить тест при известном коэффициенте корреляции.
Таблица 1. Оценка качества теста по величине rxx
|
Величина коэффициента надежности |
Качество теста |
|
0,00 – 0,599 |
Совсем неудовлетворительное |
|
0,600 – 0,699 |
Неудовлетворительное |
|
0,700 – 0,799 |
Удовлетворительное |
|
0,800 – 0,899 |
Хорошее |
|
0,900 – 0,949 |
Очень хорошее |
|
0,950 - выше |
отличное |