11.1.2. Теорема Блейка и алгоритм Блейка –Порецкого

Второй метод построения сокращенной ДНФ булевой функции основан на следующей теореме.

Теорема (Блейка). Чтобы получить сокращенную ДНФ булевой функции из произвольной ДНФ, надо выполнить всевозможные обобщенные склеивания смежных конъюнкций, а затем всевозможные поглощения конъюнкций.

Рассмотрим основанный на теореме Блейка алгоритм, который организует поиск сокращенной ДНФ эффективнее, чем это предложено в теореме.

Алгоритм Блейка –Порецкого.

Начало. Задана произвольная ДНФ булевой функции.

Шаг 1. Построим список троичных векторов, представляющих конъюнкции ДНФ. Удалим из списка все векторы, поглощаемые другими. Если останется лишь один вектор, пойдем на конец. Иначе обозначим второй из оставшихся векторов через α.

Шаг 2. Найдем для вектора α очередной смежный вектор β среди векторов, расположенных в списке выше α. Если такого вектора β нет, то идем на шаг 5. Иначе обобщенно склеим α и β и полученный вектор γ припишем к списку последним.

Шаг 3. Если вектор γ поглощается хотя бы одним вектором из списка, то удалим γ (в частном случае γ может совпадать с одним из векторов списка, тогда удалим именно приписанный вектор γ, иначе произойдет "зацикливание" алгоритма, так как вектор γ будет вновь появляться в списке) и идем на шаг 2. Если вектор γ не поглощается, то удалим все векторы, поглощаемые им.

Шаг 4. Если вектор α не удален, то идем на шаг 2.

Шаг 5. Если вектор α был не последним в списке, то выберем в качестве нового α следующий по списку вектор и вернемся на шаг 2.

Конец. Неудаленные векторы задают сокращенную ДНФ функции.

Алгоритм Блейка-Порецкого отличается от рассмотренного ранее алгоритма Квайна-МакКласки прежде всего тем, что оперирует с произвольной ДНФ, в то время как алгоритм Квайна-МакКласки требует на входе совершенную ДНФ. Конечно, можно перейти от произвольной ДНФ к совершенной, как показано в подразделе 8.2, но она может быть очень длинной, и применение алгоритма Квайна-МакКласки станет неэффективным.

Пример. Продемонстрируем алгоритм Блейка-Порецкого, сопровождая его выполнение матрицами Грея.

Начало. Задана произвольная ДНФ функции из примера к алгоритму Квайна –МакКласки:

ДНФ = a b c d a b c d a b c d a b d a b c a c d.

Шаг 1. ДНФ представляем списком векторов и нумеруем их.

Вычеркиваем из списка третий вектор, поглощаемый шестым (левая из матриц на следующей странице демонстрирует это поглощение). Остальные векторы не поглощаются (правая матрица демонстрирует состояние списка). Выбираем в качестве α второй вектор.

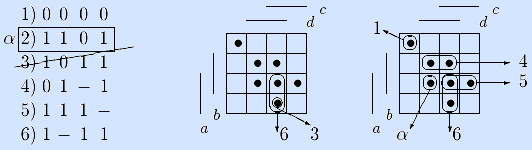
Шаг 2. Для α нет смежного вектора среди предыдущих, идем на шаг 5.

Шаг 5. Так как вектор α был не последним в списке, то в качестве нового α рассматриваем следующий по списку (четвертый) вектор (см. ниже) и возвращаемся на шаг 2.

Шаг 2. Вектор α не смежен первому вектору, но смежен второму (по первой компоненте). Обозначаем второй вектор через β. Обобщенно склеиваем α и β и записываем результат – вектор γ в список седьмым. Отмечаем, что он получен из четвертого и второго (левая нижняя матрица показывает склеивание).

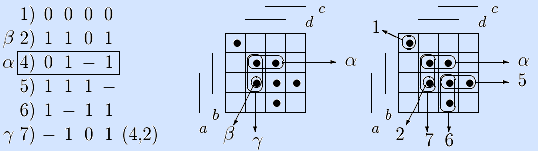
Шаг 3. Вектор γ не поглощается ни одним вектором, поэтому остается в списке. Удаляется второй вектор как поглощаемый вектором γ.

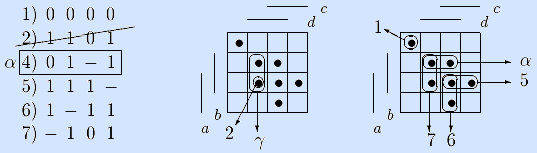
Шаг 4. Так как вектор α не был удален, идем на шаг 2.

Шаги 2, 5. Так как для вектора α перебраны все предыдущие, то идем на шаг 5. Так как α был не последним в списке, то в качестве нового α рассматриваем пятый вектор (см. ниже) и возвращаемся на шаг 2.

Шаги 2 –4. Вектор α не смежен первому, но смежен четвертому вектору β. Обобщенно склеиваем α и β и записываем результат γ в список восьмым. Вектор γ не поглощается ни одним вектором, поэтому остается в списке. Вектор γ не поглощает ни один вектор, в том числе α. Идем на шаг 2.

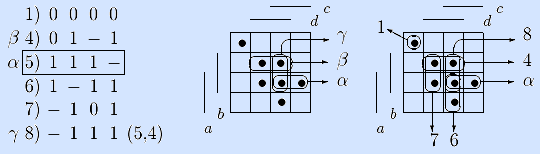
Шаги 2, 5. Для вектора α перебраны все предыдущие, поэтому новым α становится шестой вектор, идем на шаг 2.

Шаги 2 –3. Вектор α смежен четвертому вектору β (см. ниже). Обобщенно склеиваем α и β и записываем результат γ в список девятым. Вектор γ совпадает с восьмым вектором, то есть поглощается им, поэтому тут же удаляем вектор γ из списка. Идем на шаг 2.

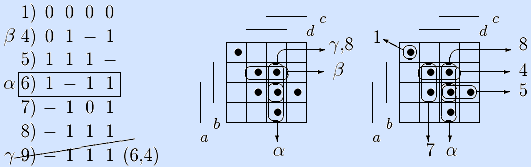
Шаги 2, 5. Для вектора α больше нет смежных среди предыдущих, поэтому новым α будет седьмой вектор, идем на шаг 2.

Шаги 2 –4. Вектор α смежен пятому вектору β. Обобщенно склеиваем их и записываем результат γ в список десятым. Вектор γ не поглощается ни одним из предыдущими векторов списка и не поглощает ни один вектор, поэтому идем на шаг 2.

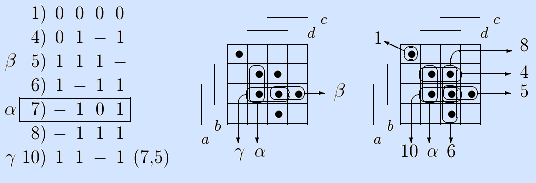
Шаги 2 –3. Вектор α смежен шестому вектору β. Обобщенно склеиваем их и записываем результат γ в список одиннадцатым. Вектор γ совпадает с десятым вектором, поэтому тут же удаляем γ из списка. Идем на шаг 2.

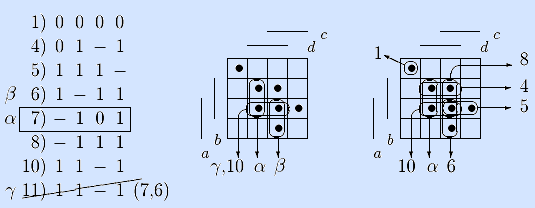
Шаги 2, 5. Так как для α перебраны все предыдущие, то в качестве нового α рассматриваем восьмой вектор и идем на шаг 2.

Шаги 2 –4. Вектор α смежен только седьмому вектору β. Обобщенно склеиваем их и записываем результат γ в список двенадцатым. Вектор γ поглощает четвертый, седьмой, восьмой и десятый векторы, поэтому удаляем их из списка. Так как вектор α оказался вычеркнутым, идем на шаг 5.

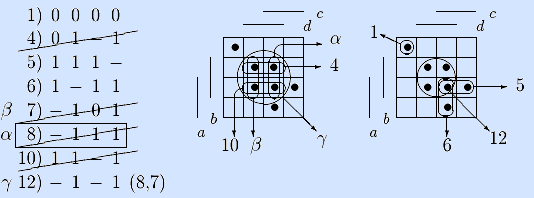
Шаг 5. Выбираем в качестве нового α двенадцатый вектор и идем на шаг 2.

Шаги 2, 5. Так как для двенадцатого вектора нет смежных среди предыдущих, то идем на шаг 5. Вектор был последним в списке, поэтому идем на конец.

Конец. Невычеркнутые из списка векторы задают сокращенную ДНФ:

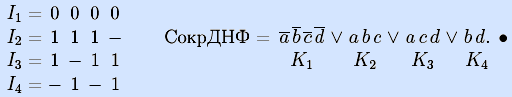
Результат совпадает с сокращенной ДНФ, полученной ранее (подраздел 11.1.1) алгоритмом Квайна-МакКласки, и это естественно, так как сокращенная ДНФ булевой функции единственна.

Демонстрируя алгоритм на примере, мы многократно переписывали списки, незначительно изменяя их на каждом шаге. Покажем, как можно ограничиться одним списком, вычеркивая поглощаемые векторы и добавляя новые. Договоримся при вычеркивании вектора сообщать номер поглощающего его вектора.

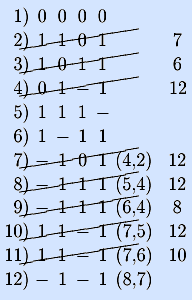
Оставшиеся в списке векторы образуют решение. •

Итак, нами изучен первый этап минимизации булевых функций – построение сокращенной ДНФ: