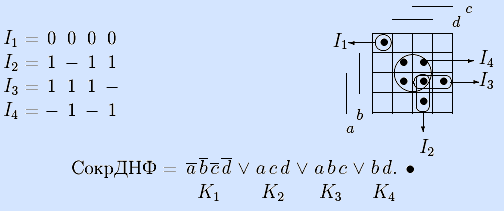11.1.1. Теорема Квайна и алгоритм Квайна –МакКласки

Первый метод построения сокращенной ДНФ булевой функции основан на следующей теореме.

Теорема (Квайна). Чтобы получить сокращенную ДНФ булевой функции из ее совершенной ДНФ, надо выполнить всевозможные неполные склеивания соседних конъюнкций, а затем всевозможные поглощения конъюнкций.

Опираясь на теорему Квайна, МакКласки сформулировал алгоритм, который организует построение сокращенной ДНФ более эффективно, чем это предложено в теореме.

Во-первых, конъюнкции в алгоритме представляются булевыми и троичными векторами, что делает вычисления более простыми и более приспособленными для компьютерной реализации.

Во-вторых, соседние векторы отличаются по весу (числу единичных компонент) ровно на единицу. Поэтому в алгоритме не проверяются на возможность склеивания векторы, чьи веса равны или отличаются более чем на единицу.

В-третьих, соседние вектора поглощаются результатом их склеивания. Поэтому отметка склеиваемых соседей (но не вычеркивание их, так как один и тот же вектор может быть соседом нескольким векторам) позволяет свести поглощение к выписыванию неотмеченных векторов.

Алгоритм Квайна –МакКласки.

Начало. Задана совершенная ДНФ булевой функции.

Шаг 1. Построим список всех точек функции (булевых векторов) и упорядочим их по неубыванию числа единиц – веса.

Шаг 2. Разобьем список на подмножества (классы) векторов одинакового веса. Обозначим через C_i класс векторов веса i.

Шаг 3. Выполним неполные склеивания всех соседних векторов классов C_i и C_i+1, i = 0,1, …, n-1. Участвующие в склеивании векторы (α и β) отметим, а полученные векторы (γ) занесем в новый список и приведем в нем подобные.

Шаг 4. Если новый список векторов не пуст, возвратимся с ним на шаг 2 (заметим, что троичные векторы списка оказываются уже упорядоченными по числу единиц).

Конец. Выписав из всех списков неотмеченные векторы, получим множество всех максимальных интервалов, оно задает сокращенную ДНФ исходной функции.

Пример. Продемонстрируем выполнение алгоритма, для наглядности сопровождая его шаги матрицами Грея.

Начало. Задана совершенная ДНФ булевой функции:

СовДНФ = a b c d a b c d a bcd a b c d abcd abcd ab cd.

Шаги 1, 2. Совершенную ДНФ представляем списком точек, упорядочиваем их по весу и разбиваем на классы.

Шаг 3. Выполняя неполные склеивания векторов из классов C₂ и C₃, а затем C₃ и C₄, и отмечая в упорядоченном списке 0 склеиваемые векторы символом *, получаем список 1 – список интервалов, состоящих из двух точек. Справа в новом списке указаны номера векторов – участников склеивания. Интервалы списка изображены на двух матрицах Грея.

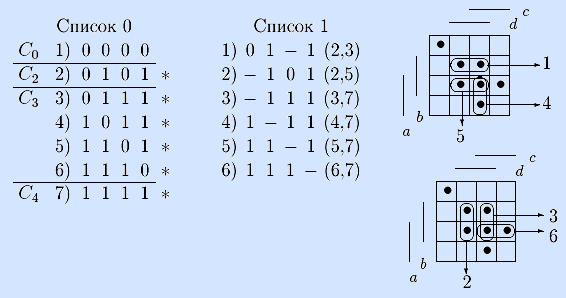
Шаг 4. Список 1 не пуст, поэтому идем на шаг 2 (так как склеивания производились в строгом порядке ''сверху вниз'', векторы в новом списке уже упорядочены по весу).

Шаги 2, 3. Разбиваем полученный список на классы C₂, C₃. Выполняя склеивания векторов из классов C₂ и C₃, получаем список интервалов, состоящих из четырех точек (список 2). Приводим в нем подобные.

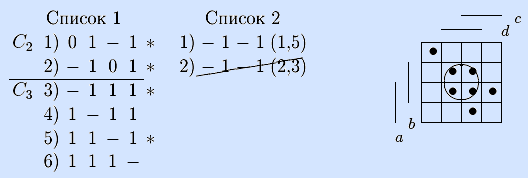
Шаг 4. Список 2 не пуст, но дальнейшее склеивание невозможно, поэтому список 3 окажется пустым, идем на конец.

Конец. Выписываем из всех списков неотмеченные векторы. Они задают сокращенную ДНФ: