4.5 Дуополия Курно
Предположим, что оба игрока уверены в отсутствии реакции со стороны конкурента на свои действия.
Данная ситуация называется дуополией Курно.

|
|
Модель дуополии, в которой оба игрока считают, что выпуск
конкурента никоим образом не зависит от объема выпуска самого игрока, называется дуополией Курно.
|
Это означает, что все предположительные вариации равны нулю, т. е.
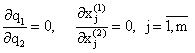 , ,
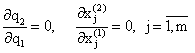 . .
Дальнейшее изложение основных особенностей модели дуополии Курно разберем на примере.
Пример

|
|
Будем предполагать, что цена единицы выпуска зависит от предложения продукции на рынке линейно, т. е.:
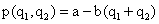 , где , где 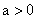 и
и 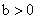 . Будем предполагать, что оба дуополиста производят товар с одинаковыми издержками,
зависящими линейно от объема выпуска: . Будем предполагать, что оба дуополиста производят товар с одинаковыми издержками,
зависящими линейно от объема выпуска:
 тогда прибыли фирм:
тогда прибыли фирм:
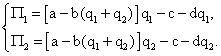 Считая предположительные вариации равными нулю, запишем необходимые условия экстремума в виде
Считая предположительные вариации равными нулю, запишем необходимые условия экстремума в виде
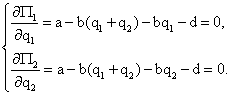 Перепишем данную систему следующим образом:
Перепишем данную систему следующим образом:
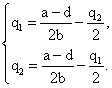 Здесь первое уравнение определяет наилучший выпуск первого дуополиста в ответ на произвольный выпуск второго
(кривую наилучших ответов первого игрока), а второе – наоборот: наилучший ответ второго игрока на действия первого
(кривую наилучших ответов второго игрока).
Здесь первое уравнение определяет наилучший выпуск первого дуополиста в ответ на произвольный выпуск второго
(кривую наилучших ответов первого игрока), а второе – наоборот: наилучший ответ второго игрока на действия первого
(кривую наилучших ответов второго игрока).
В силу симметричности ситуации, очевидно, что 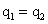 . Легко получить, что . Легко получить, что
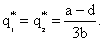 При этом на рынке установится цена
При этом на рынке установится цена 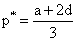 , а прибыли игроков будут одинаковы
и равны , а прибыли игроков будут одинаковы
и равны 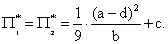 Тройка чисел
Тройка чисел 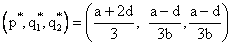 называется равновесием Курно.
На графике сложившаяся ситуация может быть представлена следующим образом: называется равновесием Курно.
На графике сложившаяся ситуация может быть представлена следующим образом:
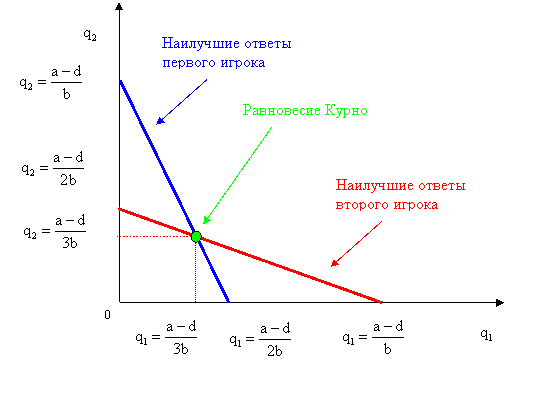 Рис. 13. - Равновесие Курно.
Рис. 13. - Равновесие Курно.
|
|

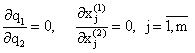 ,
,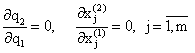 .
. 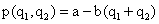 , где
, где 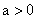 и
и 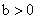 . Будем предполагать, что оба дуополиста производят товар с одинаковыми издержками,
зависящими линейно от объема выпуска:
. Будем предполагать, что оба дуополиста производят товар с одинаковыми издержками,
зависящими линейно от объема выпуска:

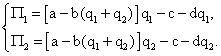
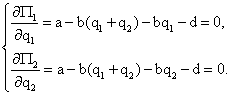
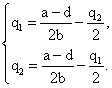
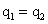 . Легко получить, что
. Легко получить, что
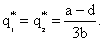
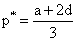 , а прибыли игроков будут одинаковы
и равны
, а прибыли игроков будут одинаковы
и равны 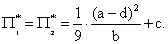 Тройка чисел
Тройка чисел 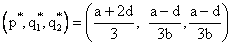 называется равновесием Курно.
На графике сложившаяся ситуация может быть представлена следующим образом:
называется равновесием Курно.
На графике сложившаяся ситуация может быть представлена следующим образом:
