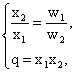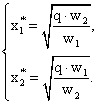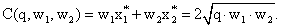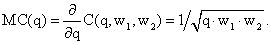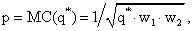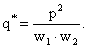3.4 Решение задачи производителя в долгосрочном периоде

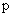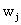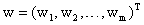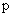Пусть - цена единицы продукции, выпускаемой фирмой, и - цена единицы затрат j-го фактора производства, так что - представляет собой вектор цен затрат. Предполагается, что цель фирмы заключается в максимизации прибыли путём выбора видов и количества затрат при заданной технологии производства продукции производственной функции и ценах и .

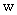Математически задачу производителя в долгосрочном периоде можно записать следующим образом:

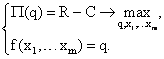
Здесь 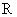- выручка от реализации выпуска продукции в размере 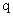единиц, 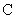- стоимость производства данного выпуска. В качестве ограничения выступает существующая технология производства продукции (производственная функция).

Очевидно, что 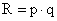, , 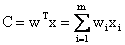где 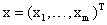- вектор затрат факторов производства.

Решение задачи производителя осуществляется в два этапа:

1. Отыскание функции издержек.

На данном этапе необходимо определить зависимость издержек производства продукции от объема выпуска. Иначе говоря, производитель должен определить, с какими минимальными издержками он может осуществить выпуск продукции заданного объема q. Минимизация издержек осуществляется за счет выбора объемов потребления факторов производства.

Задача нахождения функции издержек может быть записана следующим образом:

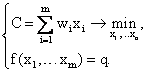
Данная задача представляет собой задачу нелинейного программирования.

Для решения этой задачи составим функцию Лагранжа:

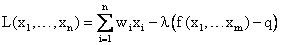
и найдем ее точки минимума. Точки, в которых функция Лагранжа достигает своего минимума, находятся среди стационарных точек, удовлетворяющих условиям:

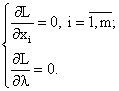
Имеем

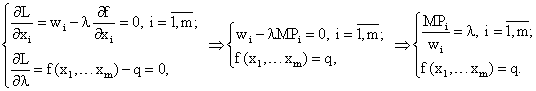
Отсюда получаем условия первого порядка минимизации издержек производства: в точке, где издержки производства минимальны, отношение предельных продуктов любых двух факторов производства должно совпадать с отношением цен этих факторов:

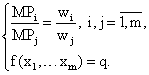
Решением данной системы уравнений являются функции спроса на факторы производства:

Эти функции спроса позволяют определить объемы потребления факторов производства в зависимости от их цен и объема выпуска продукции.

Функция издержек равна совокупной стоимости потребляемых факторов производства и, следовательно:

Введем понятия средних издержек и предельных издержек.

Средними издержками производства 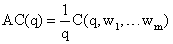называют издержки приходящиеся, в среднем, на выпуск одной единицы продукции при общем объеме выпуска q.

Предельными издержками производства 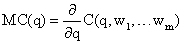называют издержки, приходящиеся на выпуск каждой дополнительной единицы продукции при общем объеме выпуска q.

2. Максимизация прибыли производителя

На данном этапе, зная с какими минимальными издержками, он может осуществить выпуск заданного объема продукции, производитель выбирает такой объем выпуска q, который бы обеспечивал ему максимальную прибыль.

Задача максимизации прибыли имеет следующий вид:

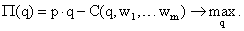
Точкой максимума прибыли будет стационарная точка функции 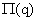, которая определяется из условия:

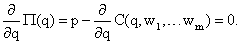
Отсюда мы получаем, что максимум прибыли производителя обеспечивает такой объем выпуска продукции 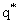, при котором цена единицы выпуска совпадает с предельными издержками данного объема выпуска:

.

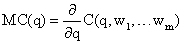Данное уравнение называют решением производителя в условиях совершенной конкуренции.

Пример

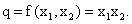
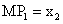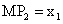Предположим, что для производства продукции используются два фактора и производственная функция имеет вид: В этом случае, предельные продукты факторов производства , и условия минимума издержек производства приобретают следующий вид: и, следовательно, функции спроса на факторы производства имеют вид: Отсюда получаем, что функция издержек: Предельные издержки производства: Отсюда определяем оптимальный объем выпуска: