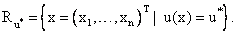2.5 Кривые безразличия
Множество наборов товаров, обеспечивающих потребителю заданный уровень полезности (являющихся одинаково
полезными для потребителя) называют
Для простоты будем предполагать, что в распоряжении потребителя имеются два вида товара:
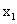 - количество единиц первого товара,
- количество единиц первого товара,
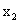 - количество единиц второго товара.
- количество единиц второго товара.
Функция полезности потребителя 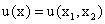 .
.
Рассмотрим основные свойства кривых безразличия:
1. Кривые безразличия, соответствующие различным уровням полезности, не пересекаются и не имеют общих точек. Это утверждение непосредственно следует из определения кривой безразличия.
2. В случае, когда предпочтения потребителя обладают свойством ненасыщаемости, чем дальше на северо-восток на координатной плоскости располагается кривая безразличия, тем более высокому уровню полезности она соответствует.
3. Кривая безразличия представляет собой график убывающей функции.
Докажем это утверждение. Запишем уравнение кривой безразличия в виде:
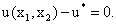
Данное тождество задает 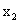 как неявную функцию от аргумента
как неявную функцию от аргумента
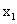 .
.
Используя правило дифференцирования неявной функции, находим производную 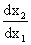 :
:
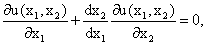
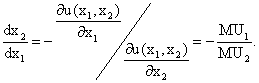
Поскольку из свойств функции полезности следует, что предельные полезности являются неотрицательными величинами,
то, следовательно, в левой части равенства стоит неположительная величина. Это означает, что 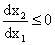 , т. е.
зависимость
, т. е.
зависимость 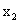 от
от 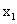 представляет собой убывающую функцию.
представляет собой убывающую функцию.
4. В случае стандартных предпочтений потребителя, кривая безразличия представляет собой график выпуклой вниз функции.
Вспомним, что функция 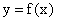 называется выпуклой вниз, если для любых значений аргумента
называется выпуклой вниз, если для любых значений аргумента 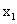 и
и 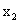 имеет место следующее соотношение:
имеет место следующее соотношение:
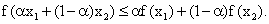
Достаточным условием выпуклости функции вниз является то, что 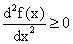 .
.
Докажем наше утверждение. Снова запишем уравнение кривой безразличия в виде:
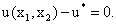
Снова будем рассматривать 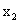 как неявную функцию от аргумента
как неявную функцию от аргумента
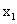 . Найдем вторую производную
. Найдем вторую производную 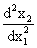 :
:

Из свойств функции полезности следует, что: 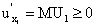 ,
,
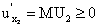 ,
, 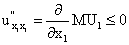 ,
,
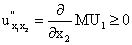 . Таким образом, мы получаем, что
. Таким образом, мы получаем, что 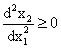 и кривая безразличия действительно представляет собой график выпуклой вниз функции.
и кривая безразличия действительно представляет собой график выпуклой вниз функции.

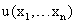 и
и
 - выбранный потребителем уровень полезности,
тогда кривой безразличия уровня
- выбранный потребителем уровень полезности,
тогда кривой безразличия уровня 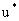 называют множество наборов товаров
называют множество наборов товаров