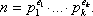 Из первого условия можно записать:
Из первого условия можно записать: 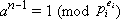 для любого
для любого 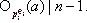 Из второго условия следует, что найдётся j, для которого
Из второго условия следует, что найдётся j, для которого 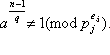 Значит,
Значит, 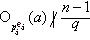 . Следовательно, имеет место делимость
. Следовательно, имеет место делимость 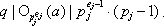 Но в силу условия (q, n) = 1 выполнено также
Но в силу условия (q, n) = 1 выполнено также 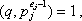 поэтому
поэтому Метод основан на теореме Диемитко.
Теорема Диемитко (1988 г.)
Пусть
1)
2)
то найдется простой делитель p числа n, для которого верно условие
Доказательство.
Пусть 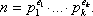 Из первого условия можно записать:
Из первого условия можно записать: 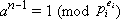 для любого
для любого 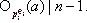 Из второго условия следует, что найдётся j, для которого
Из второго условия следует, что найдётся j, для которого 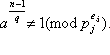 Значит,
Значит, 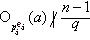 . Следовательно, имеет место делимость
. Следовательно, имеет место делимость 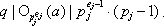 Но в силу условия (q, n) = 1 выполнено также
Но в силу условия (q, n) = 1 выполнено также 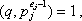 поэтому
поэтому
Следствие. Если, в условиях теоремы Диемитко, R – чётное и
Доказательство.
Предположим, что
Полученное противоречие доказывает следствие.