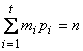7.3. Разбиения числа

Определение. Разбиением целого числа n называется мультимножество {m₁•p₁, ..., m_k•p_k} такое, что p_i>0, m_i≥0 и .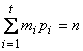

Mультимножеством называется неупорядоченная выборка с повторениями.

Запись {m₁•p₁, ..., m_k•p_k} обозначает, что мультимножество содержит m_i элементов p_i.

В отличие от композиций и разложений порядок элементов в разбиении не важен! Учитывая это упорядочим элементы в разбиении в порядке убывания, т.е. так, что p₁>p₂>…>p_k.

Пример. Разбиения числа 5, представленные ввиде мультимножеств и соответствующих им сумм.

{5•1} = 1+1+1+1+1,

{1•2, 3•1} = 2+1+1+1,

{2•2, 1•1} = 2+2+1,

{1•3, 2•1} = 3+1+1,

{1•3, 1•2} = 3+2,

{1•4, 1•1} = 4+1,

{1•5} = 5.

Разбиения числа удобно представляются с помощью диаграмм Ферререса. В диаграмме разбиения числа n = a₁ + a₂ +…+ a_k, состоящего из k частей (слагаемых), будет k строк, причем i-я будет содержать ровно a_i точек. Заметим, что длина любой строки не превышает длин вышележащих строк.

Определение. Сопряженным разбиением к заданному называется разбиение, полученное путем транспонирования (строки становятся столбцами) диаграммы Феррерса для исходного разбиения.

Заметим, что число точек при транспонировании не изменяется, т.е. полученная диаграмма представляет разбиение того же числа.

Пример. На рис 7.3.1 показаны сопряженные диаграммы Феррерса для разбиения n = 12 = 5 + 3 + 3 + 1 (диаграмма зеленого цвета) и для разбиения n = 12 = 4 + 3 + 3 + 2 (диаграмма красного цвета).     Рис. 7.3.1. Диаграммы Феррерса для сопряженных разбиений

Утверждение 7.4. Число разбиений числа n на k слагаемых равно числу разбиений числа n с наибольшим слагаемым, равным k.

Доказательство.

Каждому разбиению числа n на k частей взаимно однозначно соответствует сопряженное ему разбиение, в диаграмме которого первая (самая длинная) строка состоит из k точек. В свою очередь число строк в диаграмме сопряженного разбиения равно наибольшему слагаемому в исходном разбиении.

Определение. Разбиение называется симметричным, если его диаграмма совпадает с диаграммой сопряженного разбиения (Рис. 7.3.2a). Рис. 7.3.2. a) диаграмма симметричного разбиения; b) диаграмма соответствующего разбиения на различные нечетные слагаемые

Утверждение 7.5. Число симметричных разбиений числа n равно числу его разбиений на нечетные различные слагаемые.

Доказательство.

Перестроим диаграмму симметричного разбиения следующим образом. "Разогнем" прямой угол до 180 градусов так, чтобы точки столбца и одноименной строки лежали на одной прямой (рис.7.3.2). Из симметричности диаграммы следует, что в каждой строке в результате получится нечетное число точек, которое как минимум на две меньше, чем в предыдущей строке. Количество точек не изменится, следовательно, новая диаграмма будет представлять разбиение того же числа.

В обратную сторону доказывается аналогично. От диаграммы, состоящей из строк различной нечетной длины, перейдем к симметричной. Оставляя из каждой строки ("половину" + 1) точек на горизонтали, а остальные дописывая по вертикали, получим равенство соответствующих строк и столбцов.

Таким образом, установлено взаимно однозначное соответствие между симметричными разбиениями числа n и его разбиениями на нечетные различные слагаемые. Следовательно, их число совпадает.

Утверждение 7.6. Каждому разбиению числа n на попарно различимые слагаемые взаимно однозначно соответствует его разбиение на нечетные слагаемые.

Доказательство.

Пусть n = m₁p₁ + m₂p₂ +…+ m_kp_k, где p_i – нечетные. Представим каждое m_i в виде суммы степеней двойки, после чего просто раскроем скобки. Получим разбиение числа n на слагаемые вида p_i2^j, т.е. произведение нечетного числа на степень двойки. Любое натуральное число можно представить в таком виде единственным образом. Предположим, что это не так. Пусть p_i2^j = p_t2^q и j>q, тогда p_i2^j-q = p_t, что противоречит нечетности p_t. Следовательно, так как все p_i нечетные и различные верно, что все слагаемые в разбиении различные.

В обратную сторону соответствие доказывается аналогично. Пусть n = p₁ + p₂ +…+ p_k, где p_i – различные. Представим каждое p_i в виде произведения нечетного числа на степень двойки. Затем перегруппируем слагаемые по одинаковым нечетным сомножителям, в результате получим разбиение из нечетных слагаемых.

Пример к доказательству утверждения 7.6.

Переход от разбиения на нечетные слагаемые к разбиению на различные.
n = 43 = 9 + 3*5 + 5*3 + 4*1 = 9 + 5(2⁰ + 2¹) + 3(2⁰ + 2*2¹) + 1*2² = 9 + 5 + 10 + 3 + 6 + 4.

От разбиения на различные слагаемые к разбиению на нечетные.
n = 30 = 15 + 6 + 4 + 3 + 2 = 15*2⁰ + 3*2¹ + 1*2² + 3*2⁰ + 1*2¹ = 15 + 3(2¹ + 2⁰) + 1(2² + 2¹) = 15 + 3*3 + 5*1.

Обозначим p_k(n) число разбиений числа n ровно на k слагаемых (Иногда используется обозначение ). Очевидно, что число разбиений числа n не превосходит числа его композиций (в композициях порядок важен), следовательно, p_k(n)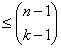. С другой стороны, каждое разбиение дает не более k! композиций (переставляем местами слагаемые, но некоторые из них повторяются), следовательно, 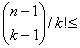p_k(n). 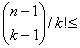Таким образом, имеет место оценка p_k(n).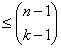

Определим значения p_k(n) для некоторых n и k.

p₀(0) = 1,

p_k(n) = 0, если k > n,

p₁(n) = 1,

p_n(n) = 1,

p₂(n) = .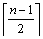

Для k > 2 выведем рекуррентную формулу.

Утверждение 7.7. Для числа разбиений числа n на k слагаемых (1 < k < n) выполняется тождество

p_k(n) = p_k(n – k) + p_k – 1(n – k)+…+ p₁(n – k).

Доказательство.

Первые три тождества очевидны. Разобьем множество рассматриваемых разбиений на классы по числу единиц в разбиении. Пусть t число единиц в разбиениях t-го класса, t = 0, …, k - 1. Вычтем из каждого слагаемого в разбиении по 1, получим разбиение числа (n - k) на (k - t) слагаемых, так как единицы обратятся в 0, т.е. в t-м классе имеем p_{k - t}(n - k) разбиений. По правилу суммы получаем требуемое соотношение.

Если ограничиться разбиением множества разбиений числа n лишь на два класса (первый содержит разбиения, в которых наименьшее слагаемое равно 1, а второй – все остальные), то рекуррентная формула примет вид:

p_k(n) = p_k-1(n – 1) + p_k(n – k).

Рассуждая аналогичным образом, покажем, что число разбиений числа n на не более чем k слагаемых равно p_k(n + k). Рассмотрим некоторое разбиение из t слагаемых, где t ≥ k. Прибавим к каждому слагаемому по единице. В результате получим разбиение числа n + k ровно на k слагаемых.

Заметим, что число разбиений числа n с наибольшим слагаемым, равным k, по утверждению 7.4 также равно p_k(n). В свою очередь, число разбиений на не более чем k слагаемых равно числу разбиений, слагаемые в которых не превосходят k.

Основным методом решения задач на разбиения числа с разного рода ограничениями является сведение их к задачам о разбиении меньших чисел или на меньшее число слагаемых, т.е. к построению рекуррентных соотношений. Другой подход требует знакомства с аппаратом производящих функций.