Существуют два основных формата представления чисел в памяти компьютера. Один из них используется для кодирования целых чисел, а второй для кодирования действительных чисел. Целые числа представляются в формате с фиксированной запятой, а действительные - в формате с плавающей точкой. Мы с вами уже говорили о том, что алфавит компьютера состоит всего лишь из двух знаков: 0 и 1. Все числа в компьютере и представляются с помощью этих двух знаков. Если говорить о том, как мы с вами записываем числа, то легко заметить, что мы это делаем всего лишь с помощью десяти цифр: 0, 1, 2, 3, 4, 5, 6, 7, 8 и 9. Например, число 234 означает, что в числе 2 сотни, 3 десятка и 4 единицы:
Другими словами, мы с вами работаем с числами в позиционной системе счисления и представляем число как сумму цифр умноженных на соответствующую степень десяти, то есть в десятичной системе счисления. Компьютер же работает с числами, записанными в двоичной системе. В этой системе счисления всего лишь две цифры: 0 и 1, а числа записываются по степеням двойки. Например, число пять кодируется как 101, потому что
 |
| Cистема счисления - искусственная информационная система, созданная с целью выработки наиболее удобного способа записи чисел. Позиционными называют системы счисления, в которых вклад каждой цифры в величину числа зависит от её положения (позиции) в последовательности цифр, изображающей число. |
| |
В десятичной системе счисления используют 10 цифр: 0,1,2,3,4,5,6,7,8 и 9. Вклад каждой цифры в число определяется ее местом расположения . Самая крайняя цифра вносит вклад пропорциональный 100, вторая с конца цифра - 101, третья - 102 и т.д. Подробнее о системах счисления Вы можете прочитать во второй теме нашего учебника. |
| |
По словам знаменитого математика и физика XVIII - XIX веков П.Лапласа: "Мысль выражать все числа десятью знаками, придавая им, кроме значения по форме, еще значение по месту, настолько проста, что именно из-за этой простоты трудно понять, насколько она удивительна". |
Нижний индекс 2, показывает, что речь идет о двоичной системе счисления. Полезно запомнить, как представляются в двоичной системе десятичные цифры.
| Десятичная цифра | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| Двоичное число | 0 | 1 | 10 | 11 | 100 | 101 | 110 | 111 | 1000 | 1001 |
Каждый регистр арифметического устройства компьютера, каждая ячейка памяти представляет собой совокупность однородных элементов, каждый из которых может принимать два состояния и используется для записи соответствующего разряда числа. Нумерацию разрядов в ячейке принято вести справа налево.
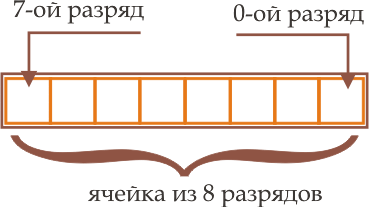
Положительные (беззнаковые) числа представляют во всех разрядах ячейки. 
Для представления целого числа со знаком используют все разряды ячейки, кроме старшего. Если в старшем разряде расположена 1, то число имеет знак минус, а если 0, то знак - плюс. . Отметим, что отрицательные числа в компьютере представляются дополнительным кодом. Более подробно о компьютерном представлении чисел можно прочитать в четвертой теме данного учебника.
|
|||||||||||||||||
 |
Pассмотрим представление числа 235 на 8-разрядной ячейке. Поскольку 235=(11101011)2, то его представление на 8-разрядной ячейке следующее:
Рассмотрим представление числа 38 на 8-разрядной ячейке. 38=(100110)2, в представлении числа 6 цифр, значит число нужно дополнить незначащими нулями слева. Представление числа 38 на 8-разрядной ячейке следующее:
|
||||||||||||||||
|
|||||||||||||||||
| |
Pассмотрим представление чисел 9 и -9 на 8-разрядной ячейке. 9=(1001)2, значит представление числа 9 на 8-разрядной ячейке со знаком следующее:
|
||||||||||||||||
Вещественные числа представляются в компьютере в нормализованной (экспоненциальной) записи , при этом часть ячеек отводится под мантиссу, а часть под порядок. Более подробно о представлении чисел можно прочитать в четвертой теме данного учебника.
| |
Нормализованная запись отличного от нуля действительного числа - это запись вида
a=±m * p q,
где m - правильная p-ичная дробь, у которой первая цифра после запятой не равна нулю;
q - целое число. m называют мантиссой, а q - порядком. |
|
|
| |
Примеры записи чисел в нормализованном виде
|