Определение. ДНФ булевой функции f(x1, …, xn) называется безызбыточной ДНФ (БезДНФf), если из нее нельзя удалить ни одной конъюнкции и ни одной переменной из конъюнкции так, чтобы она оставалась равносильной исходной ДНФ.
В частности, безызбыточной является любая минимальная и любая кратчайшая ДНФ (не простая кратчайшая ДНФ явно избыточна).
Методы поиска безызбыточных ДНФ будут рассмотрены далее. Здесь же мы найдем безызбыточную ДНФ по матрице Грея. Для этого выделим такое достаточное множество максимальных интервалов, чтобы при удалении любого интервала оно переставало быть достаточным.
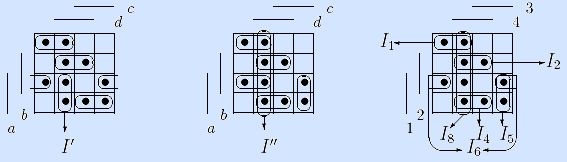
Примеры. Рассмотрим функцию из предыдущего примера.

Слева выделено достаточное множество из пяти интервалов, ни один из которых нельзя удалить так, чтобы множество оставалось достаточным. Но интервал I' – не максимальный, так как он может быть расширен по первой компоненте, то есть из конъюнкции K' = a c d можно удалить переменную a. Поэтому ДНФ, состоящая из конъюнкций, заданных этими интервалами, не является безызбыточной, но если упростить K', то ДНФ станет безызбыточной и совпадет с МинДНФ из предыдущего примера.
В центре выделено достаточное множество из шести максимальных интервалов, которое является избыточным, так как интервал I'' может быть удален, а множество при этом останется достаточным. Поэтому ДНФ, состоящая из конъюнкций, заданных шестью выделенными интервалами, не является безызбыточной, но если удалить интервал I'', то ДНФ станет безызбыточной и совпадет с кратчайшей ДНФ из предыдущего примера.
Справа выделено достаточное множество If из шести максимальных интервалов (с номерами из предыдущего примера). Удаление любого из них приводит к тому, что множество перестает быть достаточным. Поэтому множество If задает безызбыточную ДНФ (длины 6, ранга 17):
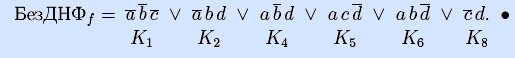
Сравнение длин и рангов ДНФ из двух последних примеров, показывает, что эта безызбыточная ДНФ не является ни кратчайшей, ни минимальной.
Обратим внимание, что все конъюнкции, задаваемые ядерными интервалами (в нашем примере это интервалы I1 и I2), входят во все безызбыточные ДНФ, в том числе во все кратчайшие и минимальные ДНФ.