МинДНФ_f =КратДНФ_f =z x y (длины 2, ранга 3).

Однако эта функция имеет еще одну кратчайшую ДНФ:

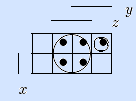КратДНФ'_f = z x y z (длины 2, ранга 4).

КратДНФ'_f отличается от КратДНФ_f тем, что ее вторая конъюнкция не является простой импликантой, ее можно упростить вычеркиванием z . •

Теорема о кратчайшей ДНФ. Существует кратчайшая ДНФ булевой функции, состоящая из простых импликант.

Доказательство (конструктивное). Рассмотрим произвольную булеву функцию f(x₁, …, x_n). Докажем сначала вспомогательный результат. Пусть функция g(x₁, …, x_n) – импликанта функции f(x₁, …, x_n), тогда

Если g(x₁, …, x_n)=0, то обе части этого выражения равны f(x₁, …, x_n). Если g(x₁, …, x_n)=1, то и f(x₁, …, x_n)=1 (так как g(x₁, …, x_n) – импликанта функции f(x₁, …, x_n)), а значит, обе части равны 1. Рассмотрим теперь КратДНФ_f функции f(x₁, …, x_n).

Если все ее конъюнкции являются простыми импликантами функции, то кратчайшая ДНФ, состоящая из простых импликант, найдена. Иначе пусть K₁ – не простая импликанта функции f(x₁, …, x_n), тогда существует простая импликанта K'₁ такая, что K₁ K'₁=K'₁. По доказанному верно

Длина КратДНФ'_f равна длине КратДНФ_f. Повторив те же рассуждения для всех остальных конъюнкций КратДНФ'_f, мы получим кратчайшую ДНФ функции f(x₁, …, x_n), состоящую из простых импликант. •

Определение. Назовем простой кратчайшей ДНФ булевой функции f(x₁, …, x_n) ее кратчайшую ДНФ, состоящую из простых импликант.

Далее из всех кратчайших ДНФ нас будут интересовать только простые кратчайшие ДНФ, так как помимо минимальной длины они имеют и меньший ранг каждой конъюнкции. Однако называть и обозначать простые кратчайшие ДНФ функции f(x₁, …, x_n) будем по-прежнему – КратДНФ_f.

Пример. Рассмотрим функцию f(x,y,z), которая имеет две простые кратчайшие ДНФ.

s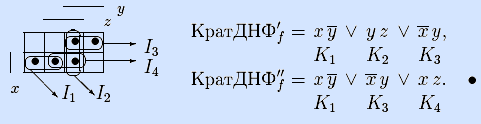

Для минимальных ДНФ справедливо более сильное утверждение, чем для кратчайших.

Теорема о минимальных ДНФ. Любая минимальная ДНФ булевой функции состоит из простых импликант.

Доказательство (от противного). Рассмотрим произвольную функцию f(x₁, …, x_n). Предположим, что в ее минимальной ДНФ по крайней мере одна из конъюнкций не является простой импликантой функции.

Пусть K₁ – не простая импликанта функции f(x₁, …, x_n), тогда найдется ее простая импликанта K'₁ такая, что K₁ K'₁=K'₁. Как было показано при доказательстве предыдущей теоремы, если в МинДНФ_f заменить конъюнкцию K₁ на конъюнкцию K'₁ то получившаяся ДНФ_f будет равносильна исходной. При этом ДНФ_f будет иметь меньший ранг, чем МинДНФ_f, так как конъюнкция K'₁ имеет меньший ранг, чем K₁ что противоречит тому, что МинДНФ_f является минимальной ДНФ функции f(x₁, …, x_n). •

Итак, если булева функция задана матрицей Грея, то:

– для построения сокращенной ДНФ необходимо выделить все максимальные интервалы;

– для построения кратчайшей ДНФ – их достаточное множество минимальной мощности;

– для построения минимальной ДНФ – такое достаточное множество максимальных интервалов, сумма рангов которых минимальна.

Примеры. Найдем сокращенную, кратчайшие и минимальные ДНФ функции f(a,b,c,d):

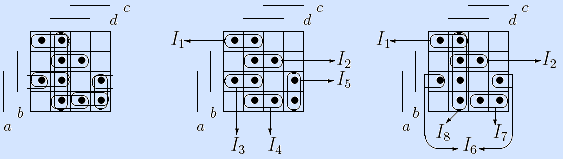
На левой матрице показано множество всех максимальных интервалов (их номера можно найти на двух других матрицах).

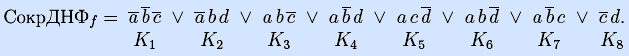
В центре показано достаточное множество из пяти максимальных интервалов {I₁,I₂,I₃,I₄,I₅}. Никакие четыре из восьми максимальных интервалов не образуют достаточного множества, следовательно, ДНФ, состоящая из конъюнкций, заданных интервалами I₁ – I₅, является кратчайшей (длины 5, ранга 15):

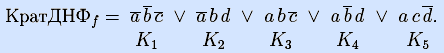
Справа показано достаточное множество из пяти максимальных интервалов {I₁,I₂,I₆,I₇,I₈}. Никакое другое достаточное множество не дает меньшей суммы рангов, следовательно, соответствующая ДНФ является минимальной (длины 5, ранга 14):

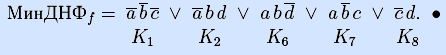
Обратим внимание, что в данном случае КратДНФ_f не является минимальной, а МинДНФ_f является кратчайшей. Других кратчайших и минимальных ДНФ эта функция не имеет (напомним, что мы рассматриваем только простые кратчайшие ДНФ).