9.1. Импликанты функции и сокращенная ДНФ

Рассмотрим булевы функции f(x₁, …, x_n) и g(x₁, …, x_n).

Определение. Булева функция g(x₁, …, x_n) называется импликантой функции f(x₁, …, x_n), если

g(x₁, …, x_n) f(x₁, …, x_n) ≡ 1.

Так как x y = 0 только на наборе 10, то для того, чтобы функция g(x₁, …, x_n) была импликантой функции f(x₁, …, x_n) достаточно, чтобы на всех тех наборах α, на которых g(α)=1, функция f(x₁, …, x_n) также принимала значение 1.

Примеры. Пусть функция f(x,y,z) задана матрицей Грея (левая матрица на рисунке). Функция g(x, y, z) и конъюнкции K₁= x y z, K₂= z (три правые матрицы) – ее импликанты.

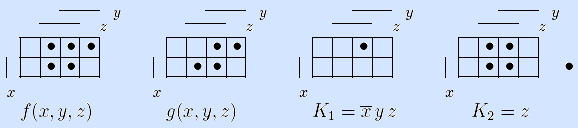
Очевидно, что если K – любая конъюнкция ДНФ_f, то K является импликантой функции f(x₁, …, x_n) и задается допустимым для функции f(x₁, …, x_n) интервалом I_K.

Определение. Элементарная конъюнкция K называется простой импликантой функции f(x₁, …, x_n),если она является импликантой этой функции, и не существует другой конъюнкции K', которая является импликантой функции f(x₁, …, x_n) и поглощает конъюнкцию K.

Примеры. Рассмотрим функцию f(x,y,z) из предыдущего примера. Конъюнкция K₂=z – простая импликанта данной функции, а конъюнция K₁= x y z – импликанта, но не простая, так как она поглощается импликантой K₂. •

Другими словами, простая импликанта функции – это такая импликанта-конъюкция, которая не может быть упрощена выбрасыванием из нее переменных, то есть неупрощаемая конъюнкция. Это означает, что всякая простая импликанта K булевой функции f(x₁, …, x_n) задается максимальным для этой функции интервалом I_K.

Определение. ДНФ, состоящая из всех простых импликант булевой функции f(x₁, …, x_n), называется сокращенной ДНФ этой функции (или СокрДНФ_f).

Из определения следует, что сокращенная ДНФ единственна для данной функции, то есть наряду с СовДНФ и СовКНФ она является еще одной канонической формой представления булевой функции.

В общем случае построение сокращенной ДНФ является довольно сложной задачей, которая будет рассмотрена нами далее. Однако для булевой функции небольшого числа аргументов, заданной матрицей Грея, найти сокращенную ДНФ (или, что то же самое, множество всех максимальных интервалов ) довольно просто, и мы уже решали такую задачу для мажоритарной функции в подразделе 3.3, изучая интервальный способ задания булевой функции.

Примеры. Найдем сокращенные ДНФ функций из предыдущего примера: f(x,y,z), g(x,y,z), и функции h(x,y,z).

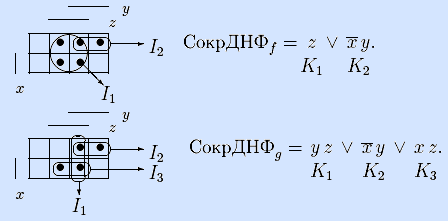
СокрДНФ_h сложнее – она состоит из шести простых импликант, поэтому для наглядности изображена на двух матрицах Грея:

Обратим внимание на то, что термин ''сокращенная'' относится не к длине ДНФ (она может быть большой, значительно больше длины совершенной ДНФ), а к рангам всех ее конъюнкций – ранги неупрощаемых конъюнкций (именно из них состоит сокращенная ДНФ) не могут быть уменьшены.