x y и идемпотентности x x = x).Алгоритм преобразования ДНФ в совершенную ДНФ (основан на законах склеивания y = xy x y и идемпотентности x x = x).
Начало: задана ДНФf функции f(x1, …, xn).
Шаг 1: рассматриваем очередную конъюнкцию K исходной ДНФf. Если все конъюнкции исчерпаны, идем на конец.
Шаг 2: если конъюнкция K не является полной, то выбираем переменную xi, которая не входит в K, и по закону склеивания заменяем K на дизъюнкцию двух конъюнкций: K = K xi Kx i (в таком применении будем называть его законом расклеивания соседних конъюнкций). Если полученные слагаемые не являются полными конюнкциями, то применяем к каждой из них закон расклеивания (шаг 2) до тех пор, пока не получим из конъюнкции K дизъюнкцию полных конъюнкций. Идем на шаг 1.
Конец: на основании закона идемпотентности приводим подобные среди одинаковых конъюнкций – получаем СовДНФ функции f(x1, …, xn).
Пример. Пусть ДНФf = x1x2 x 1x 2 x3, n = 3. Применим закон расклеивания к каждой конъюнкции:
x1x2 = x1x2 x3 x1x2 x 3,
x 1x 2 =
x 1x 2x3 x 1x 2x 3,
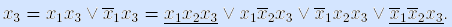
В последней строке подчеркнуты конъюнкции, совпадающие с полученными ранее. По закону идемпотентности они не войдут в совершенную ДНФ, которая примет вид
СовДНФf=
x1x2 x3 x1x2 x 3
x 1x 2x3 x 1x 2x 3
x1x 2x3
x 1x2 x3.