7.3. Совершенная дизъюнктивная нормальная форма

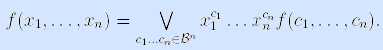
Разложив булеву функцию f(x₁, …, x_n) по k переменным при k = n, получим

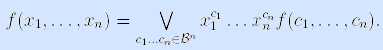
Поскольку коэффициентами разложения здесь являются значения функции на всевозможных наборах, то возможны два случая:

– либо набор c₁ … c_n M⁰_f, тогда f(c₁ …, c_n)=0, и поэтому обращается в 0 соответствующее слагаемое правой части;

– либо набор c₁ … c_n M¹_f, тогда f(c₁, …, c_n)=1, и слагаемое упрощается.

В результате имеем формулу разложения функции по всем переменным

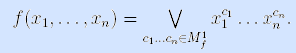
Пример. Найдем коэффициенты разложения той же булевой функции f(x,y,z)= y xz yz по всем переменным (для удобства наборы c₁ … c_n Bⁿ будем перебирать в естественном порядке):

f(0,0,0) =0 0 0 0 0 = 1 0 0 = 0 0 = 1,

f(0,0,1) =0 0 1 0 1 = 1 0 0 = 0 0 = 1,

f(0,1,0) =1 0 0 1 0 = 0 0 0 = 1 0 = 0,

f(0,1,1) =1 0 1 1 1 =0 0 1 = 1 1 = 1,

f(1,0,0) =0 1 0 0 0 = 1 1 0 = 1 0 = 0,

f(1,0,1) =0 1 1 0 1 = 1 0 0 = 0 0 = 1,

f(1,1,0) =1 1 0 1 0 = 0 1 0 = 0 0 = 1,

f(1,1,1) =1 1 1 1 1 = 0 0 1 = 1 1 = 1.

Подставив коэффициенты в формулу, получим

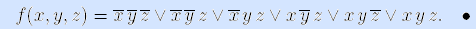
Нетрудно заметить, что вычисление коэффициентов разложения функции по всем переменным эквивалентно построчному построению ее таблицы истинности.

Определение. Совершенная дизъюнктивная нормальная форма функции f(x₁, …, x_n) (СовДНФ_f) – это формула вида

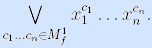
Из данной формулы с очевидностью вытекает следующее утверждение.

Утверждение о единственности совершенной ДНФ. Любая булева функция, кроме константы 0, представима cовершенной дизъюнктивной нормальной формой, единственной для данной функции.

Алгоритм построения совершенной ДНФ по таблице истинности (основан на определении совершенной ДНФ).

Начало: задана таблица истинности булевой функции.

Шаг 1: в векторе-столбце значений функции выбирается очередная единица. Если единицы исчерпаны, то идем на конец.

Шаг 2: по набору значений аргументов выбранной строки формируется конъюнкция всех аргументов с соблюдением правила: если i-я компонента набора равна 0, то i-я переменная входит в конъюнкцию в степени 0 (с инверсией), иначе – в степени 1 (без инверсии). Полученная конъюнкция добавляется в формулу как очередное слагаемое. Идем на шаг 1.

Конец.

Пример. Применим алгоритм к той же функции (с переименованными аргументами) f(x₁, x₂, x₃)=x ₂ x₁x ₃ x₂ x₃.

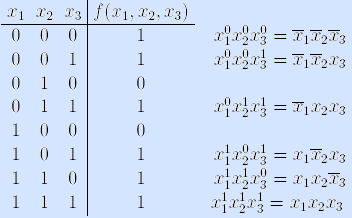
Соединив полученные конъюнкции знаками дизъюнкции, имеем

СовДНФ_f = x ₁x ₂x ₃ x ₁x ₂x₃ x ₁x₂ x₃ x₁x ₂x₃ x₁x₂ x ₃ x₁x₂ x₃.

Обратим внимание на тот факт, что нам впервые удалось перейти от табличного способа задания функции к формульному!

Решение обратной задачи, то есть построение таблицы истинности по совершенной ДНФ, очевидно: степени переменных конъюнкций совершенной ДНФ задают наборы, на которых функция принимает значение 1. Это гораздо проще, чем построение таблицы истинности по совершенной ДНФ как по произвольной формуле.