x 1f(0,x2, …, xn)=Разложим функцию f(x1, …, xn) последовательно по двум переменным: сначала саму функцию по переменной x1 затем коэффициенты разложения по переменной x2 .
x 1f(0,x2, …, xn)= x 2 f(1,0,x3, …, xn)] x 1[x2 f(0,1,x3, …, xn) x 2 f(0,0,x3, …, xn)]=[ раскроем скобки по закону дистрибутивности ]
x1x 2 f(1,0,x3, …, xn) x 1x2 f(0,1,x3, …, xn) x 1x 2 f(0,0,x3, …, xn).Введем обозначения: x = x1, x = x0 (условимся читать символы xc как ''x в степени c''). Тогда разложение функции f(x1, …, xn) по переменным x1, x2 в свернутой форме примет вид
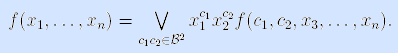
Пример. Продолжим разложение функции f(x,y,z) из предыдущего примера. Мы уже получили ее разложение по x:
xz 
yz =x (y z yz) x (y yz). Разложим теперь коэффициенты по переменной y:
z 1z) y (0 z 0z)] x [y(1 1z) y (0 0z)]=
[ используем свойства 0 и 1 и раскроем квадратные скобки ]
z z) y (1
z 0)] x [y(1 z)
y (0 0)]= z)
xy (z 0) x y z
x y = z)
xy z x y z x y .Решим теперь тот же пример, но не последовательным применением разложения Шеннона, а непосредственно по формуле разложения функции по двум переменным.
Пример. Найдем коэффициенты разложения Шеннона булевой функции f(x,y,z)=y xz yz по переменным x и y:
f(1,1,z) =1 1z 1z = 0 z z=z z;
f(1,0,z) =0 1z 0z
=1 z 0 =z 0 = z;
f(0,1,z) =1 0z 1z
=0 0 z = 1 z =z;
f(0,0,z) = 0 0z 0z = 1 0 0 = 0 0 =1.
Подставив коэффициенты разложения в формулу, получим
x1y0 f(1,0,z) x0y1 f(0,1,z) x0y0 f(0,0,z) = x y(z z) xy z x y z x y . Заметим, что в данном случае оба способа привели к одинаковым формулам. В общем случае формулы могут не совпадать, но они с очевидностью равносильны, ибо задают одну функцию.
Разложение функции по k переменным имеет вид, аналогичный разложению функции по двум переменным.
Разложение функции по k переменным.
Доказательство. Подставим в левую и правую части равенства произвольный набор a1… an:
Для упрощения правой части докажем сперва вспомогательный результат: ac=1 тогда и только тогда, когда a=c. Действительно, 00=0 =1, 11=1, но 01=0, 10=1 =0. Следовательно, конъюнкция a1c1 … akck=1 тогда и только тогда, когда a1 … ak и c1 … ck совпадают. Это означает, что конъюнкция не обращает в ноль лишь одно слагаемое правой части, для которого c1=a1 …, ck=ak, и разложение имеет вид: