 (x
(x  y z) )
y z) ) ( y
( y  x ),
x ),
Определение. Формула F* называется двойственной формуле F, если она получена из F заменой символов функций на символы двойственных им функций.
Пример.
F = x ↓ (y  (x
(x  y z) )
y z) ) ( y
( y  x ),
x ),
F* = x / (y  x (y
x (y  z))
z)) 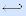 ( y
( y
 x ). •
x ). •
Теорема (принцип двойственности). Если формула F задает булеву функцию f(x1, …, xn), то двойственная ей формула F* задает двойственную функцию f*(x1, …, xn).
Доказательство. По условию теоремы формула F задает булеву функцию f(x1, …, xn). По определению формулы F имеем:
Рассмотрим двойственную ей формулу:
[ по определению двойственной функции для fi*(x1, …, xn), i=1, …, m ]
[ по определению двойственной функции для f0*(y1, …, ym) ]

[ по закону двойного отрицания ]
[ по определению двойственной функции для f(x1, …, xn ]
Пример. Рассмотрим формулу F = 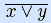 , задающую
булеву функцию НЕ-ИЛИ, то есть стрелку Пирса. Двойственная ей формула F* = x y должна задавать функцию, двойственную стрелке Пирса – это штрих Шеффера: в самом деле F* = x y – это функция НЕ-И, то есть штрих Шеффера. •
, задающую
булеву функцию НЕ-ИЛИ, то есть стрелку Пирса. Двойственная ей формула F* = x y должна задавать функцию, двойственную стрелке Пирса – это штрих Шеффера: в самом деле F* = x y – это функция НЕ-И, то есть штрих Шеффера. •
Следствие из принципа двойственности. Если формулы F1 и F2 равносильны, то двойственные им формулы F*1 и F*2, также равносильны.
Доказательство. Равносильные формулы F1 и F2задают одну и ту же булеву функцию f(x1, …, xn), следовательно, по принципу двойственности, двойственные им формулы F*1 и F*2, задают двойственную f(x1, …, xn) функцию f*(x1, …, xn). •
Таким образом, можно не доказывать некоторые равносильности (в том числе и основные), а выводить их, пользуясь следствием из принципа двойственности.
Примеры. Исходя из закона склеивания конъюнкций x y  x y = y и используя следствие, получим ( x
x y = y и используя следствие, получим ( x  y ) ( x
y ) ( x  y ) = y – закон склеивания дизъюнкций. Исходя из одного закона де Моргана
y ) = y – закон склеивания дизъюнкций. Исходя из одного закона де Моргана 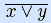 = x y и используя следствие, получим другой закон де Моргана x y = x
= x y и используя следствие, получим другой закон де Моргана x y = x  y . •
y . •