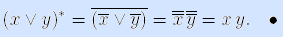Определение. Булева функция f*(x1, …, xn) называется двойственной булевой функции f(x1, …, xn), если она получена из f(x1, …, xn) инверсией всех аргументов и самой функции, то есть
f*(x1, …, xn) =f (x 1, …, x n).
Пример. Построим функцию, двойственную стрелке Пирса.
Пусть булева функция f(x1, …, xn) задана формулой Ff. Чтобы получить формулу F'f* для функции f*(x1, …, xn), двойственной функции f(x1, …, xn), необходимо, согласно определению, проинвертировать все переменные, пользуясь при этом законом двойного отрицания, и саму функцию. При этом формулу F'f* можно упростить (убрать длинную инверсию над формулой), заменив символ функции, которая вычисляется последней, на символ инверсной ей функции.
Пример. Пусть Ff = x ↓ (y 
(x 
y z) )
( y 
x ). Последней должна вычислятьси импликация, инверсная ей функция это обратная импликация, поэтому формула для двойственной функции примет вид:
Алгоритм построения таблицы истинности двойственной функции (основан на определении двойственной функции).
Инверсия всех переменных превращает наборы в их антиподы. Поскольку в таблице истинности антипод первого набора расположен последним, антипод второго набора – предпоследним и так далее, то для построения функции f(x 1, …, x n) нужно перевернуть вектор-столбец значений исходной функции f(x1, …, xn), а для получения функции f (x 1, …, x n) еще и инвертировать компоненты столбца.
Пример. Построим функцию, двойственную стрелке Пирса.
Пары двойственных элементарных функций:
0 1 , 
, ↓ / , , 
, 
.
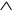Тождественная функция и инверсия двойственны каждая самой себе.
Для доказательства можно воспользоваться алгоритмом построения таблицы истинности двойственной функции (именно так предыдущий пример демонстрирует, что штрих Шеффера двойственен стрелке Пирса), или применить равносильные преобразования.
Пример. Покажем, что дизъюнкция двойственна конъюнкции (применив законы де Моргана и двойного отрицания):
