3.6. Упражнения

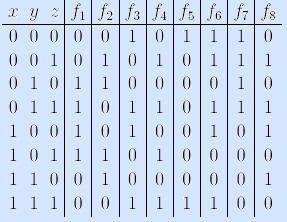
Упр.1. Задать с помощью таблиц истинности, характеристических множеств, векторов, матриц Грея и интервалов следующие булевы функции:

f₁: B³ B, функция равна единице на тех и только тех наборах, вес которых больше единицы;

f₂: B⁴ B, функция равна единице на тех и только тех наборах, которые представляют числа большие или равные 7;

f₃: B³ B, функция равна нулю на всех наборах с нечетным весом, и только на них.

Упр.2. Определить ядерные точки и интервалы булевых функций.

Упр.3. Привести примеры таблиц истинности булевых функций:

f₁: B³ B, функция принимает различные значения на противоположных наборах;

f₂: B³ B: f(α ) ≤ f(β ) если α β.

Упр.4. Соревнования обслуживают три судьи, один из них главный. Вес считается поднятым, если ''за'' проголосовало большинство судей, в том числе и главный. Построить таблицу истинности булевой функции, описывающей такое голосование.

Упр.5. Вдоль длинного коридора размещены лампы. Включение и выключение света управляется тремя выключателями, два из которых расположены в концах коридора, а третий – посередине. При нажатии любого выключателя все лампы включаются, если были выключены, и выключаются, если были включены. Построить таблицу истинности булевой функции, описывающей управление освещением коридора.

Упр.6. Найти и удалить фиктивные переменные булевых функций.

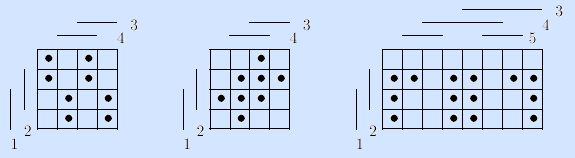
Упр.7. Найти и удалить фиктивные переменные булевых функций.

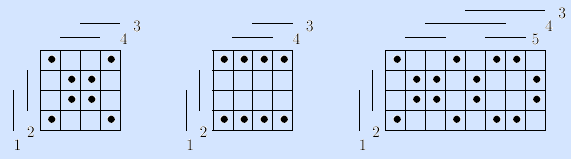
Упр.8. Представить все элементарные булевы функции матрицами Грея и разбить их на пары инверсных функций.