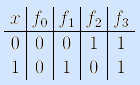
Рассмотрим все булевы функции двух и менее аргументов.
При n = 0 имеем две функции: константу 0 и константу 1.
При n = 1 имеем четыре функции:
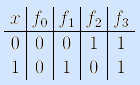
Функции f0(x) и f3(x) зависят от x несущественно, поэтому равны двум рассмотренным ранее функциям. Введем названия и обозначения для остальных двух функций:
f1(x)= x – тождественная функция (читается ''x''),
f2(x) = x – функция отрицания (инверсия, НЕ) (читается ''не x'').
При n = 2 имеем 16 функций:
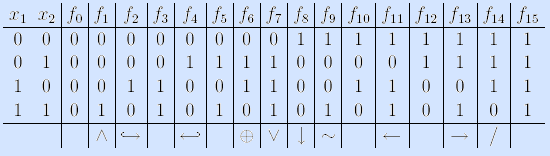
Функции f0, f3, f5, f10, f12, f15 содержат фиктивные переменные и поэтому уже рассмотрены ранее. Обозначения остальных функций указаны в нижней строке таблицы,а названия их таковы:
f1(x1, x2)=x1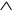
x2 – конъюнкция (логическое умножение, И) (читается ''x1 и x2 ''),
f7(x1, x2) = x1
x2 – дизъюнкция (логическое сложение, ИЛИ) (читается ''x1 или x2 ''),
f6(x1, x2) = x1
x2 – дизъюнкция с исключением (сложение по модулю 2) (читается ''x1 плюс x2 ''),
f9(x1, x2) = x1
x2 – эквивалентность (читается ''x1 эквивалентно x2 ''),
f8(x1, x2) = x1↓ x2 – стрелка Пирса (НЕ-ИЛИ) (читается ''x1 стрелка x2 ''),
f14(x1, x2) = x1/ x2 – штрих Шеффера (НЕ-И) (читается ''x1 штрих x2 ''),
f13(x1, x2) = x1
x2 – импликация (логическое следование) (читается ''x1 имплицирует x2 ''),
f2(x1, x2) = x1
x2 – не импликация (читается ''x1 не имплицирует x2 ''),
f11(x1, x2) = x1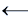
x2 – обратная импликация читается ''x1 обратно имплицирует x2 ''),
f4(x1, x2) = x1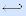
x2 – не обратная
импликация (читается ''x1 не обратно имплицирует x2 '').
Определение. Булевы функции двух и менее аргументов назовем элементарными булевыми функциями.
Пары инверсных элементарных функций:
0 1,
↓ ,
/,
,
,
,
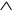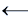
кроме того, пару составляют тождественная функция и инверсия.