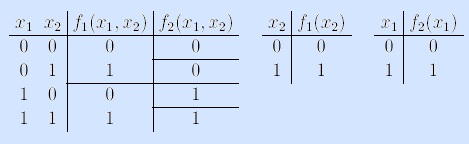Определение. Говорят, что булева функция f(x1, …, xi, …, xn) существенно зависит от переменной xi, если выполняется условие
f(x1, …, xi-1,0,xi+1, …, xn) ≠ f(x1, …, xi-1,1,xi+1, …, xn).
В этом случае также говорят, что переменная xi существенная, в противном случае ее называют фиктивной переменной.
Пример. Рассмотрим булеву функцию f(x1, x2, x3) и исследуем ее переменные x1 и x3.

Из таблиц истинности видно, что переменная x1 функции f(x1, x2, x3) существенная, так как f(0,x2, x3) ≠ f(1,x2, x3). Переменная x3 фиктивная, так как f(x1, x2, 0) = f(x1, x2, 1). •
Очевидно, что для выявления фиктивных переменных можно не строить в явном виде таблиц истинности левой и правой частей неравенства, а сравнивать соответствующие части вектора-столбца значений функции.
Алгоритм распознавания фиктивной переменной по таблице истинности.
– Для переменной x1 сравниваются половины столбца значений функции: верхняя и нижняя, так как именно в верхней половине x1=0, а в нижней x1=1, если они совпадают, то переменная x1 фиктивна;
– для переменной x2 сравниваются четвертины столбца в каждой половине, так как именно в верхних четвертинах x2 =0, а в нижних x2 =1, если четвертины в каждой половине совпадают, то переменная x2 фиктивна;
– и так далее (за четвертинами следуют 1/8, 1/16, … ).
Пример. Для булевой функции из предыдущего примера переменная x1 существенна, так как верхняя половина столбца значений функции (0011) не равна нижней половине (1100). Переменная x2 существенна, так как четвертины уже в первой половине различаются (00 и 11). Переменная x3 фиктивна, так как осьмушки во всех четвертинах равны (0 и 0, 1 и 1, 1 и 1, 0 и 0). •
Выявление фиктивных переменных можно ускорить, используя следующее очевидное утверждение.
Достаточное условие отсутствия фиктивных переменных. Если вес вектора-столбца значений функции нечетен, то функция не может содержать фиктивных переменных.
Алгоритм удаления фиктивной переменной xi состоит в вычеркивании из таблицы истинности всех строк, в которых xi = 0 (или всех строк, в которых xi = 1), и столбца xi.
Пример (функция та же). Применив алгоритм для удаления фиктивной переменой x3 (таблица слева), получаем результат (таблица справа).
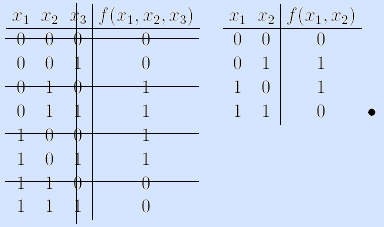
Если переменная xi функции f(x1, …, xn) фиктивна, то на наборах, соседних по i компоненте, функция принимает одинаковые значения. Отсюда следует способ выявления и удаления фиктивной переменной функции, заданной матрицей Грея.
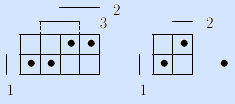
Алгоритм распознавания фиктивной переменной по матрице Грея (основан на свойстве симметрии кода Грея).
Переменная фиктивна тогда и только тогда, когда точки на матрице расположены симметрично относительно осей этой переменной. Упрощенная матрица – это одна из ее симметричных половин.
Пример (функция та же и представлена на левой матрице). Переменная x3 функции фиктивна. Справа показан результат ее удаления.
Определение. Булевы функции назовем равными с точностью до фиктивных переменных, если равны (в смысле, определенном ранее) функции, полученные из исходных удалением фиктивных переменных (и именно это расширенное толкование равенства функций мы будем иметь в виду во всех дальнейших рассуждениях).
Пример. Рассмотрим функции f1(x1, x2) и f2(x1, x2). Удалив фиктивную переменную x1 функции f1(x1, x2) и фиктивную переменную x2 функции f2(x1, x2), получим равные функции f1(x2)=f2(x1)=f(x). Значит, исходные функции равны с точностью до фиктивных переменных.