Определение. Булевым пространством Bn размерности n называется множество всех булевых векторов длины n, расстояние между которыми вычисляется по Хэммингу.
Примеры. B1 = {0,1} =B, B2={00,01,10,11}. •
Булево пространство может быть задано несколькими способами. Рассмотрим два из них.
1) Явным перечислением векторов.
Пример. B3={000, 100, 010, 001, 110, 101, 011, 111}. •
2) Матрицей в коде Грея. Булево пространство размерности n представляется матрицей, состоящей из 2s строк и 2p столбцов, где s и p – целые числа, такие что s + p = n и s = p либо s = p-1. Строкам матрицы поставлены в соответствие булевы векторы длины s (их называют кодами строк), а столбцам – булевы векторы длины p (коды столбцов).
Коды столбцов упорядочены по следующему принципу:
– младшая компонента кодов, то есть компонента с меньшим номером, равна 0 в первой половине столбцов и равна 1 во второй их половине (например, если столбцов восемь, то младшая компонента принимает значения 00001111);
– следующая компонента равна 0 в первой четверти кодов и равна 1 во второй четверти, после чего значения симметрично повторяются, то есть равны 1 в третьей четверти и 0 в четвертой (в примере: 00111100) – симметрирование происходит в момент, когда предыдущая компонента меняет свое значение с 0 на 1;
– cледующая компонента равна 0 в первой осьмушке кодов и равна 1 во второй их осьмушке, после чего ее значения дважды симметрично повторяются (в примере: 01100110) – симметрирование происходит в моменты, когда вторая компонента, а затем первая, меняют свои значения с 0 на 1;
– и так далее (за 1/8 следуют 1/16, 1/32, … ).
Коды строк строятся аналогично.
Элемент матрицы в коде Грея, стоящий в i-й строке и j-м столбце, задает булев вектор, который получается приписыванием к коду строки i кода столбца j.
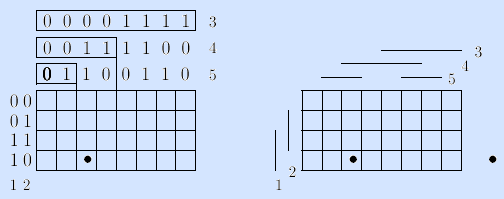
Пример. Пусть n=5. На левой матрице показан процесс построения кодов столбцов. Выделенная клетка задает булев вектор 10011.

Договоримся изображать коды условно: единицу – черточкой, а ноль – ее отсутствием: такой код более нагляден, да и быстрее рисуется (он показан на правой матрице предыдущего примера).
Код Грея обладает свойством симметрии, которое оказывается полезным при решении многих задач. Проиллюстрируем это свойство на примере матрицы для пространства B5.
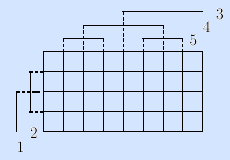
На матрице пунктирными линиями обозначены места смены значений компонент, эти линии называются осями симметрии компонент. Каждая ось имеет свою зону симметрии, то есть область, на которую распространяется ее действие:
– зоной симметрии оси младшей компоненты (в примере: первой для строк и третьей для столбцов) является вся матрица;
– зонами симметрии двух осей следующих компонент (в примере: второй для строк и четвертой для столбцов) являются половины матрицы;
– и так далее (с каждым разом размер зоны уменьшается в два раза, а число осей увеличивается в два раза).
Нетрудно заметить, что пара соседних векторов располагается в матрице симметрично относительно оси той компоненты, по которой векторы ортогональны, причем относительно именно оси, в зоне симметрии которой располагаются вектора.
Пример. Каждый из соседей выделенного вектора отмечен номером ортогональной компоненты.
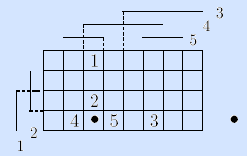
Симметричное расположение соседей на матрице Грея упрощает их поиск и делает представление булева пространства наглядным.
При описании кода Грея мы фактически изложили алгоритм его построения. Рассмотрим более простой алгоритм рисования кода Грея для столбцов матрицы (код Грея для строк рисуется аналогично).
Алгоритм рисования кода Грея для столбцов матрицы.
Начало: задана матрица из 2p столбцов.
Шаг 1: отступив от края матрицы один столбец, нарисуем черточку над двумя столбцами, затем, пропустив два столбца, нарисуем черточку над двумя следующими столбцами и так далее до конца матрицы.
Шаг 2: отступив от полученного ряда черточек немного вверх, начнем следующий ряд: нарисуем черту от середины первой до середины второй черточки предыдущего ряда, затем – от середины третьей до середины четвертой черточки предыдущего ряда и так далее до конца матрицы. Повторим шаг 2, пока это возможно (последнюю черту, которая начнется с середины матрицы, оборвем у правого края).
Конец.
Пример. Матрица содержит 16 столбцов.
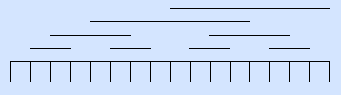
Далее будем называть матрицу в коде Грея матрицей Грея.