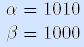1.3. Пара булевых векторов

Рассмотрим два булевых вектора одинаковой длины и договоримся для наглядности писать их один под другим

α=a₁a₂… a_n,

β=b₁b₂… b_n.

Определение. Говорят, что булевы векторы α и β ортогональны по i-й компоненте, если a_i ≠ b_i.

Пример. Векторы 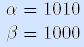ортогональны по 3-й компоненте. •

Определение. Расстоянием между булевыми векторами называют число ортогональных компонент в данной паре векторов (его еще называют расстоянием по Хэммингу).

Пример. Расстояние по Хэммингу между векторами 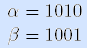равно двум. •

Определение. Булевы векторы называются соседними (соседями), если они ортогональны по одной и только одной компоненте, то есть расстояние по Хэммингу между векторами равно единице.

Пример. Векторы 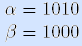– соседи (по третьей компоненте). •

Определение. Булевы векторы называются противоположными (антиподами), если они ортогональны по всем компонентам, то есть расстояние по Хэммингу между векторами равно их длине.

Пример. Векторы 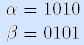– антиподы. •

Определение. Говорят, что булев вектор α = a₁a₂ … a_n предшествует булеву вектору β = b₁b₂ … b_n (и это отношение обозначают α β), если для любого i=1, 2, …, n выполняется условие a_i ≤ b_i (здесь компоненты булевых векторов интерпретируются как числа 0 и 1). В этом случае говорят также, что булев вектор β следует за α, булев вектор α называют предшественником, а β – последователем.

Пример. 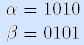: α β . •

Определение. Булевы векторы α и β называются сравнимыми, если α β или β α , в противном случае говорят, что они несравнимы.

Примеры. Рассмотрим две пары векторов 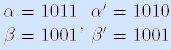. Векторы α и β сравнимы, причем β α, а α' и β' несравнимы. •