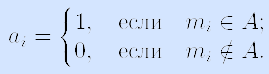
Определение. Булев вектор это последовательность булевых констант, называемых компонентами булева вектора.
Договоримся обозначать булевы векторы греческими буквами, а компоненты вектора – латинскими с указанием номеров компонент.
Примеры. α=a1a2…a6=010101, β = b1b2…b8= 11110000. •
Определение. Длиной булева вектора назовем количество его компонент, а весом вектора – количество компонент, равных единице.
Пример. Длина булева вектора α =101010 равна шести, а вес – трем. •
Теорема о числе булевых векторов. Число различных булевых векторов длины n равно 2n.
Доказательство (методом математической индукции по длине булева вектора).
База индукции: имеется два булевых вектора длины 1: это 0 и 1.
Индуктивное предположение: пусть число различных булевых векторов длины n равно 2n
Индуктивный переход: добавим к векторам длины n еще одну n+1-ю компоненту, присвоив ей сначала значение 0 (получим 2n векторов), а затем значение 1 (получим еще 2n векторов). Итого существует 2n+2n=2n+1 различных булевых векторов длины n+1. •
Примеры. Имеется 4 булевых вектора длины два: 00, 01, 10, 11, и 8 булевых векторов длины три: 000, 100, 010, 001, 110, 101, 011, 111. •
Представление булевыми векторами подмножеств. Пусть заданы множество M={m1 m2, …, mn} и его подмножество A. Построим булев вектор α = a1a2 … an, представляющий подмножество A, следующим образом:зафиксируем порядок элементов в множестве M и положим
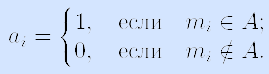
Примеры. Булев вектор α = 11101 в множестве чисел M = {2, 6, 4, 7, 8 } выделяет подмножество четных чисел, булев вектор β = 10010 выделяет в этом же множестве подмножество простых чисел.•
Представление булевыми векторами целых неотрицательных чисел. Введем соответствие между булевым вектором α = a1a2 … an и числом a {0, 1, … , 2n-1}:
{0, 1, … , 2n-1}:
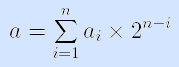
(здесь компоненты булева вектора интерпретируются как числа 0 и 1).
Примеры.
Задан булев вектор α = 1001, подставив его компоненты в формулу, получим число a = 1 × 23 + 0 × 22 + 0 × 21 + 1 × 20 = 8 + 1 = 9.
Задано число a = 13, разложив его, согласно формуле, на сумму степеней двойки: 13 = 8 + 4 + 1 = 1 × 23 + 1 × 22 + 0 × 21 + 1 × 20, получим булев вектор α = 1101. •
Данный алгоритм построения булева вектора по числу легко применим лишь для малых чисел, но в общем случае применяется другой вариант алгоритма.
Алгоритм построения вектора, представляющего число (использует целочисленное деление, результатом которого являются два целых числа: неполное частное и остаток).
Начало: задано целое число a ≥ 0.
Шаг 1: поделим a на 2, запомним неполное частное и остаток.
Шаг 2: если полученное частное не равно нулю, то поделим его на 2, запомним новые неполное частное и остаток и повторим шаг 2.
Конец: выпишем остатки в обратном порядке – получим искомый булев вектор.
Пример. a =36, 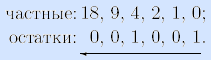
Выписав остатки в обратном порядке, получим булев вектор α = 100100, представляющий число 36.•