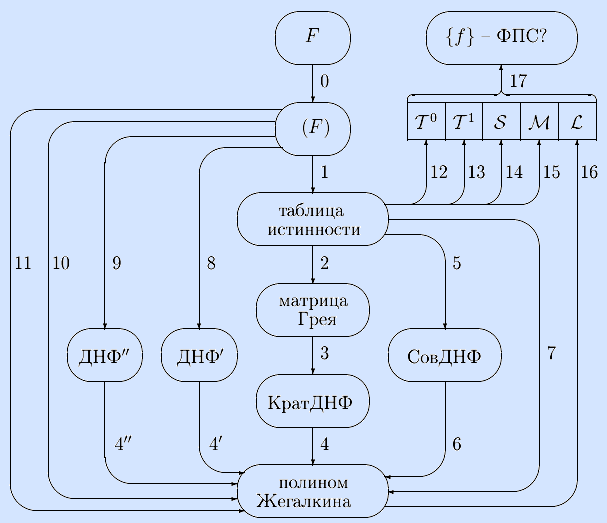
Темы контрольной работы: полиномы Жегалкина, замкнутые классы, функциональная полнота.

8 – подстановка кратчайших ДНФ элементарных функций
9 – разложение Шеннона
10 – подстановка полиномов Жегалкина элементарных функций
11 – разложение Дэвио
Схема контрольной работы (решение каждой из 20 предложенных здесь задач начинать с постановки задачи и делать вывод из сравнения полиномов Жегалкина, полученных разными способами; F означает формулу без лишних скобок, (F) – с недостающими скобками).
1)x ↓ y  x z x z |
11)x / y  y z y z |
21)x  y / y z y / y z
|
2)x  y y  x z x z |
12)x ↓ y  x z x z |
22)x / y  y z y z
|
3)x  y ↓ y z y ↓ y z |
13)x  y / x z y / x z |
23)x  y y  y z y z
|
4)x  y ↓ x z y ↓ x z |
14)x y  z / y z / y |
24)x y  z / y z / y |
5)x / y  x z x z |
15)x  y y  y z y z |
25)x / y  x z x z |
6)x ↓ y 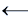 y z y z |
16)x 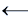 y y  x z x z |
26)x  y / y z y / y z |
7)x 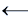 y / y z y / y z |
17)x / y  y z y z |
27)x  y y 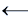 x z x z |
8)x y  z ↓ y z ↓ y |
18)x y  z z  y y |
28)x y  z z  y y |
9) y z 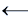 x x  y y |
19)x y  z z 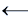 y y |
29)x y ↓ z  y y |
10)x y  y y  z z | 20)x z ↓ y / x |
30)x  y z y z  x x |
Пример. Задана формула
 x y .
x y .0) Расставим скобки в формуле F.
 (x y ).
(x y ).1) Построим таблицу истинности функции f(x,y,z) по формуле (F).

2) Построим матрицу Грея по таблице истинности.
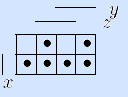
3) Получим кратчайшую ДНФ функции по ее матрице Грея.
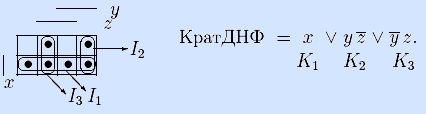
4) Получим полином Жегалкина функции по кратчайшей ДНФ.
 yz
yz  y z=
y z=[ дизъюнкцию пары ортогональных конъюнкций
yz  y z
заменим на их дизъюнкцию с исключением ]
y z
заменим на их дизъюнкцию с исключением ]
 ( yz
( yz  y z)=
y z)=
[ применим равносильность A1 A2= A1
A2= A1 A2
A2 A1A2
при A1=x, A2=yz
A1A2
при A1=x, A2=yz  y z ]
y z ]
 yz
yz  y z
y z
 x(yz
x(yz  y z)
=x
y z)
=x  yz
yz  y z
y z
 xyz
xyz  xy z=
xy z=
[ заменим каждую переменную с инверсией a
равносильной формулой a  1, раскроем скобки
и удалим пары одинаковых конъюнкций ]
1, раскроем скобки
и удалим пары одинаковых конъюнкций ]
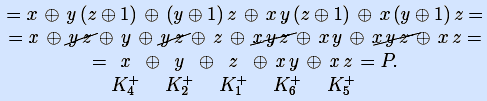
Конъюнкции здесь и во всех последующих задачах пронумерованы согласно представлению полинома Жегалкина в форме с коэффициентами.
5) Получим совершенную ДНФ по таблице истинности.
 x yz
x yz  xy z
xy z  xy z
xy z xyz
xyz  xyz.
xyz.
6) Получим полином Жегалкина по совершенной ДНФ.
 x yz
x yz  xy z
xy z  xy z
xy z xyz
xyz  xyz=
xyz=
[ заменим все знаки дизъюнкции на знаки дизъюнкции с исключением ]
 x yz
x yz  xy z
xy z  xy z
xy z xyz
xyz  xyz=
xyz=
[ заменим каждую переменную с инверсией a
равносильной формулой a  1, раскроем скобки
и удалим пары одинаковых конъюнкций ]
1, раскроем скобки
и удалим пары одинаковых конъюнкций ]
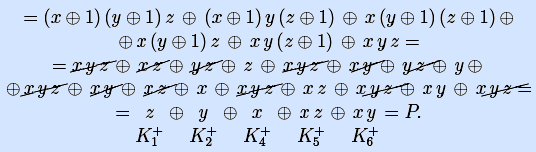
7) Получим полином Жегалкина по таблице истинности. Используем метод неопределенных коэффициентов, последовательно вычисляя коэффициенты полинома и подставляя их в остальные уравнения. Вектор коэффициентов π полинома выпишем под таблицей.

8) Получим ДНФ' по формуле (F) подстановкой кратчайших ДНФ элементарных булевых функций.
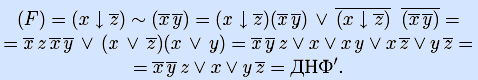
4') Получим полином Жегалкина функции по ДНФ' (как в задаче 4).
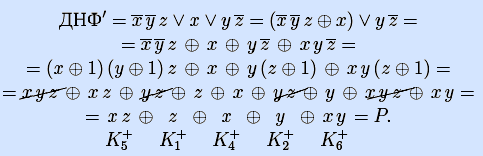
9) Получим ДНФ'' по формуле (F) разложением Шеннона.
 (x y )=
x[(1 ↓ z )
(x y )=
x[(1 ↓ z )  (0y )]
(0y )]
 x [(0 ↓ z )
x [(0 ↓ z )  (1y )]=
(1y )]= 0]
0]  x [z
x [z y ]=
x
y ]=
x  x [z(1
x [z(1  y )
y ) z (0
z (0  y )]=
y )]= x y z
x y z x yz
=ДНФ'.
x yz
=ДНФ'.4'') Получим полином Жегалкина функции по ДНФ'' (аналогично задаче 4 и учитывая, что все конъюнкции попарно ортогональны).
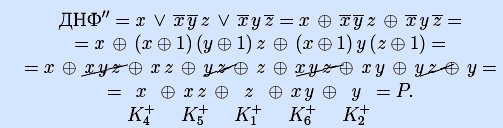
10) Получим полином Жегалкина по формуле (F) подстановкой полиномов Жегалкина элементарных булевых функций.
 (x y )=
(x y )=
[ найдем полином Жегалкина стрелки Пирса
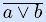 =1
=1  a
a  b
b  a b
a b
и подставим его в формулу при a=x, b = z ]
 x
x  z
z  xz )
xz )  (x y )=
(x y )=
[ найдем полином Жегалкина эквивалентности
 b =
b =  =1
=1  a
a  b
b
и подставим его в формулу при a=1  x
x  z
z  xz ,
b = x y ]
xz ,
b = x y ]
 (1
(1  x
x  z
z  xz )
xz )  (x y )=
(x y )=
[ избавимся от скобок, инверсий и пар одинаковых конъюнкций ]
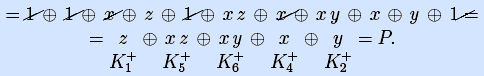
11) Получим полином Жегалкина по формуле (F) разложением Дэвио.
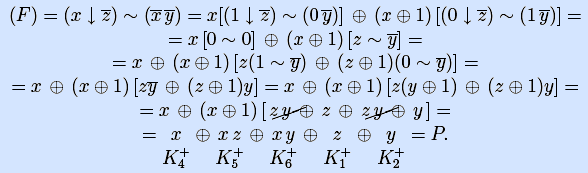
Вывод. Полиномы Жегалкина, полученные семью различными способами, совпадают, следовательно, задачи 1) –11) с большой вероятностью решены верно.
12 –15) Определим, принадлежит ли функция замкнутым классам T0, T1, S и M, по таблице истинности.
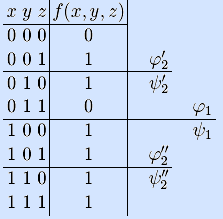
Так как
f(0,0,0)=0, то функция сохраняет константу 0,
f(x,y,z) T0.
T0.
Так как f(1,1,1)=1, то функция
сохраняет константу 1,
f(x,y,z) T1.
T1.
Число единиц в столбце значений функции не равно числу нулей,
значит, выполняется достаточное условие несамодвойственности,
f(x,y,z)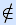 S.
S.
Верхняя половина столбца значений функции предшествует нижней:
φ1=0110  1111=φ1
но четвертина φ'2=01 не предшествует
четвертине
φ'2=10, значит,
функция не монотонна,
f(x,y,z)
1111=φ1
но четвертина φ'2=01 не предшествует
четвертине
φ'2=10, значит,
функция не монотонна,
f(x,y,z)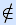 M.
M.
16) Определим, принадлежит ли функция классу L
по полиному Жегалкина.
P=z  y
y  x
x  x z
x z  x y, степень полинома
равна двум, значит, функция нелинейна, f(x,y,z)
x y, степень полинома
равна двум, значит, функция нелинейна, f(x,y,z)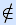 L.
L.
17) Определим, образует ли функция f(x,y,z) функционально полную систему. Из задач 12) –16) следует, что вектор непринадлежности функции замкнутым классам имеет вид:
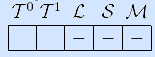
Функция не образует функционально полную систему по теореме Поста –Яблонского, так как принадлежит классам T0 и T1. •