16.2. Упражнения

Упр. 1. Используя теорему о двух ФПС, показать, что системы функций являются функционально полными:

N₁={x yz,0},

N₃={x y,x y z },

N₂={x ( y z )},

N₄={x y,0}.

Упр. 2. Исследовать функцию g(x,y,z) из последнего примера на ее непринадлежность пяти замкнутым классам.

Упр. 3. Построить таблицы непринадлежности функций каждого из заданных множеств замкнутым классам и проверить, являются ли множества функционально полными.

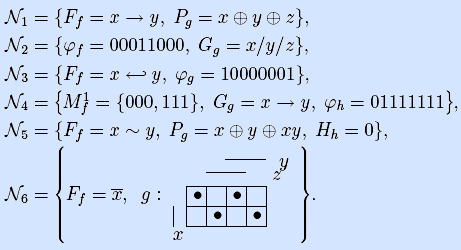
Упр. 4. Какие элементарные булевы функции необходимо добавить в системы, чтобы они стали функционально полными? Не использовать штрих Шеффера и стрелку Пирса.

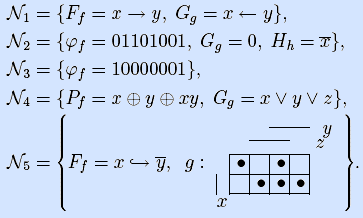
Упр. 5. Проверить функциональную полноту систем булевых функций. Удалить из каждой системы максимальное количество функции таким образом, чтобы она оставалась функционально полной.

Упр. 6. Проверить правильность построения таблицы непринадлежности элементарных булевых функций пяти замкнутым классам.