16.1. Необходимые и достаточные условия функциональной полноты
Перейдем к рассмотрению одного из основных вопросов теории
булевых функций – вопроса о необходимых и достаточных условиях полноты
систем булевых функций. Этот вопрос важен как с теоретической
точки зрения, ибо математика всегда интересует вопрос о
возможности выражения одних функций через другие, так и с
практической точки зрения, при выборе так называемой
элементной базы для построения логических схем.
База должна быть функционально полной, чтобы из ее элементов можно
было построить схемы, реализующие любые булевы функции.
Пример. Любую булеву функцию можно реализовать
логической схемой из стрелок Пирса, так как множество
N={↓ }, как показано в предыдущем примере,
функционально полно. •
Теорема Поста –Яблонского. Для того, чтобы система
булевых функций N была функционально
полной, необходимо и достаточно, чтобы она не
содержалась целиком ни в одном из пяти замкнутых классов
T0, T1, L, S и M,
то есть чтобы система булевых функций N содержала хотя бы одну функцию,
не сохраняющую константу 0, хотя бы одну функцию,
не сохраняющую константу 1, хотя бы одну нелинейную,
хотя бы одну несамодвойственную и хотя бы одну немонотонную функции.
Доказательство необходимости. Дано:
функционально полная система N.
Доказать, что множество N не
содержится целиком ни в одном из пяти замкнутых классов.
Докажем сначала, что N содержит хотя бы одну несамодвойственную
функцию. Предположим противное, пусть в N все функции
самодвойственны. Так как класс
самодвойственных функций замкнут, то любая суперпозиция
самодвойственных функций является самодвойственной, и
никакая несамодвойственная функция не может быть представлена
такой суперпозицией. Следовательно, N не является ФПС,
что противоречит условию теоремы. Это означает, что N содержит хотя
бы одну несамодвойственную функцию.
Аналогично можно показать, что
N содержит хотя бы одну функцию,
не сохраняющую константу 0, хотя бы одну функцию,
не сохраняющую константу 1, хотя бы одну нелинейную,
и хотя бы одну немонотонную функции.
Доказательство достаточности. Дано: множество N,
которое не
содержится целиком ни в одном из пяти замкнутых классов.
Доказать, что N – ФПС.
Введем следующие обозначения для функций множества N:
f0 –
функция, не сохраняющая константу 0;
f1 –
функция, не сохраняющая константу 1;
fL –
нелинейная функция;
fS –
несамодвойственная функция;
fM –
немонотонная функция.
Рассмотрим два множества функций: N1={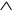 , –}
и заданное множество N, и применим к ним теорему
о двух ФПС. N1 является ФПС, как было показано в
одном из предыдущих примеров;
N будет ФПС, если каждая из
функций N1 представима
суперпозицией функций из N. Покажем, что конъюнкцию и
инверсию можно выразить через функции f0 ,
f1 , fL , fS ,
fM , используя леммы о функции, не сохраняющей
константу 0, о нелинейной, несамодвойственной и немонотонной
функциях.
, –}
и заданное множество N, и применим к ним теорему
о двух ФПС. N1 является ФПС, как было показано в
одном из предыдущих примеров;
N будет ФПС, если каждая из
функций N1 представима
суперпозицией функций из N. Покажем, что конъюнкцию и
инверсию можно выразить через функции f0 ,
f1 , fL , fS ,
fM , используя леммы о функции, не сохраняющей
константу 0, о нелинейной, несамодвойственной и немонотонной
функциях.
Следующая схема наглядно демонстрирует доказательство.
В ней следом за знаком функции в квадратных скобках показаны
допустимые по условиям леммы подстановки, а после знака равенства –
получаемый по лемме результат.
Начнем с функции
f0 : по лемме о функции, не
сохраняющей константу 0, подстановкой вместо аргументов функции
переменной x получим либо константу 1, либо x .
Проанализируем первый случай
(верхняя ветвь схемы). Имея константу 1 и
подставляя ее вместо каждого аргумента функции
f1 , получим константу 0. Затем по лемме о
немонотонной функции, подставляя в функцию
fM вместо аргументов полученные константы и
переменную x, получим x . Таким образом, инверсия
выражена суперпозицией функций f0 ,
f1 и fM .
Перейдем ко второму случаю (нижняя ветвь схемы).
Инверсия уже получена из функции f0 .
По лемме о несамодвойственной функции,
подставляя в fS вместо аргументов
переменную x и ее инверсию x ,
получим либо
константу 0, либо константу 1. Если имеем константу 0, то,
подставляя ее вместо каждого аргумента функции
f0 , получим константу 1 (средняя ветвь).
Если имеем константу 1, то,
подставляя ее вместо каждого аргумента функции
f1 , получим константу 0 (нижняя ветвь).
Таким образом, следуя по любой из трех ветвей схемы, мы получаем константы
0 и 1 и инверсию. Далее по лемме о нелинейной функции, подставляя в
функцию fL константы 0 и 1, переменные x,
y и их инверсии x , y и, возможно,
инвертируя саму функцию, получим конъюнкцию xy.
Итак, мы показали, что конъюнкция и инверсия представимы
суперпозицией функций из N, значит,
N – ФПС. •
Пример 1. Ранее мы получили, что N1={↓ }
является ФПС, значит, по теореме Поста –Яблонского
стрелка Пирса не должна принадлежать ни одному из замкнутых
классов, и это действительно так. •
Пример 2. Как показано в таблице непринадлежности
элементарных функций замкнутым классам, штрих Шеффера,
как и стрелка Пирса, не
принадлежит ни одному замкнутому классу, значит,
N2={/} – ФПС. •
Пример 3. Рассмотрим множество N3={0, }.
Импликация принадлежит только классу T1, поэтому вместе с
константой 0, не принадлежащей этому классу, образует ФПС N3.
•
}.
Импликация принадлежит только классу T1, поэтому вместе с
константой 0, не принадлежащей этому классу, образует ФПС N3.
•
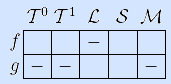
Пример 4. Рассмотрим теперь множество неэлементарных
булевых функций N4={f,g}.
Непринадлежность функций f и g пяти
замкнутым классам
представлена таблицей (мажоритарная функция f
рассматривалась нами в примерах к пяти замкнутым классам,
исследование функции g
оставляем читателям).
Так как обе функции являются самодвойственными, то система N4 не является
функционально полной. Но если к ней добавить несамодвойственную функцию, например,
константу 1, то получим ФПС N5={f,g,1}. •
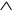 , –}
и заданное множество N, и применим к ним теорему
о двух ФПС. N1 является ФПС, как было показано в
одном из предыдущих примеров;
N будет ФПС, если каждая из
функций N1 представима
суперпозицией функций из N. Покажем, что конъюнкцию и
инверсию можно выразить через функции f0 ,
f1 , fL , fS ,
fM , используя леммы о функции, не сохраняющей
константу 0, о нелинейной, несамодвойственной и немонотонной
функциях.
, –}
и заданное множество N, и применим к ним теорему
о двух ФПС. N1 является ФПС, как было показано в
одном из предыдущих примеров;
N будет ФПС, если каждая из
функций N1 представима
суперпозицией функций из N. Покажем, что конъюнкцию и
инверсию можно выразить через функции f0 ,
f1 , fL , fS ,
fM , используя леммы о функции, не сохраняющей
константу 0, о нелинейной, несамодвойственной и немонотонной
функциях.
 }.
Импликация принадлежит только классу T1, поэтому вместе с
константой 0, не принадлежащей этому классу, образует ФПС N3.
•
}.
Импликация принадлежит только классу T1, поэтому вместе с
константой 0, не принадлежащей этому классу, образует ФПС N3.
•