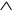16. Функциональная полнота системы булевых функций

Определение. Множество функций N называется функционально полной системой (ФПС), если любая булева функция представима суперпозицией функций из N.

Договоримся опускать аргументы при перечислении функций множества N и рассматривать термин ''система'' в данном контексте как синоним множества.

Пример 1. Множество N₁={, , 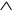^–} является функционально полной системой, так как любую булеву функцию, кроме константы 0, можно представить совершенной ДНФ, то есть суперпозицией функций из N₁ а константу 0 – формулой xx . •

Пример 2. Множество N₂={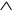, , 1} является ФПС, так как любую булеву функцию можно представить полиномом Жегалкина, то есть суперпозицией функций из N₂, а полином 0 – формулой 1 1. •

Следующая теорема позволяет сводить вопрос о функциональной полноте одних систем к вопросу о полноте других систем.

Теорема о двух функционально полных системах. Если даны два множества N₁ и N₂ булевых функций и известно, что N₁ – функционально полная система, а каждая функция из N₁ представима суперпозицией функций из N₂, то N₂тоже является функционально полной системой.

Доказательство. Рассмотрим произвольную булеву функцию f(x₁, …, x_n). Она может быть представлена суперпозицией функций из множества N₁={f₀,f₁ …, f_m}, так как N₁ – ФПС:

По условию теоремы каждая из функций f₀, f₁ …, f_m может быть представлена суперпозицией функций из N₂, значит, функция f(x₁, …, x_n) представима суперпозицией функций из N₂, следовательно, N₂ – ФПС. •

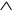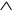Пример 1. N₁={ , ^–,}, N₂={, ^–}. Как показано ранее, N₁ – ФПС. Конъюнкция и инверсия содержатся в N₂, а дизъюнкция представима суперпозицией функций из N₂: x y = 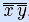, значит, N₂ – ФПС. •

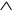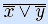Пример 2. N₁={, ^–}, N₂={↓ }. Как показано в предыдущем примере, N₁ – ФПС. Инверсия и конъюнкция могут быть представлены суперпозицией стрелки Пирса: x = x↓ x, xy == (x↓ x)↓ (y↓ y), следовательно N₂ – ФПС. •