
Определение. Булева функция f(x1, …, xn) самодвойственна (принадлежит классу S), если она равна двойственной себе функции, то есть
Примеры. Мажоритарная функция самодвойственна:

Из элементарных функций самодвойственными являются лишь тождественная функция и инверсия. Остальные функции, в частности, штрих Шеффера и стрелка Пирса, несамодвойственны. •
Алгоритм распознавания самодвойственной функции, заданной таблицей истинности. Очевидно, что для проверки самодвойственности булевой функции можно не получать двойственную ей функцию в явном виде, а лишь сравнивать значения исходной функции на противоположных наборах. Функция самодвойственна, если и только если на противоположных наборах принимает противоположые значения.
Достаточное условие несамодвойственности булевой функции. Если число единиц в столбце значений функции не совпадает с числом нулей, то функция не является самодвойственной.
Доказательство очевидно. •
Примеры. Рассмотрим три булевы функции.
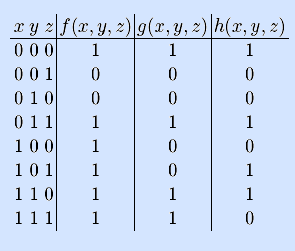
Для функции f(x,y,z) выполняется достаточное условие несамодвойственности. Для остальных оно не выполняется, при этом функция g(x,y,z) несамодвойственна, так как на первом и последнем наборах принимает одинаковые значения, а функция h(x,y,z) самодвойственна. •
Утверждение о числе самодвойственных булевых функций. Число различных самодвойственных булевых функций, зависящих от n переменных, равно 22n –1.
Доказательство. Рассмотрим самодвойственную функцию n аргументов, заданную таблицей истинности. Если на первом наборе она принимает значение a, то, согласно свойству самодвойственной функции, на последнем наборе (противоположном первому) она принимает значение a . То же можно сказать о втором и предпоследнем наборах, и так далее. Таким образом, сасодвойственная функция полностью определяется верхней половиной своего столбца значений, то есть булевым вектором длины 2n/2=2n –1. Следовательно, число различных самодвойственных функций n переменных равно 22n –1. •
Пример. Из всех 16 булевых функций двух аргументов x1, x2 4 функции (222 –1) принадлежат классу S: тождественные функции x1 и x2 и их инверсии x 1 и x 2. •
Теорема о замкнутости класса S. Множество всех самодвойственных булевых функций является замкнутым классом.
Доказательство. Рассмотрим суперпозицию любых булевых функций из S, то есть функцию
и покажем, что она самодвойственна. Пользуясь принципом двойственности, получим функцию, двойственную f(x1, …, xn).
[ учтем, что каждая из функций, образующих суперпозицию, самодвойственна ]
Итак, мы показали, что f*(x1, …, xn)=f(x1, …, xn), значит, f(x1, …, xn) самодвойственна, и класс S замкнут. •
Лемма о несамодвойственной булевой функции. Если булева функция несамодвойственна, то из нее подстановкой вместо аргументов переменной x и ее инверсии x можно получить либо константу 0, либо константу 1.
Доказательство. Рассмотрим несамодвойственную булеву функцию f(x1, …, xn). Для нее существует такой набор a1… an, что
Заменим каждый аргумент xi функции f(x1, …, xn на xai, (подстановка переменной x и ее инверсии x допустима по условию теоремы). В результате получим функцию одного аргумента
Покажем, что она является константой. Заметим, что 0a = a , 1a=a (проверка предоставляется читателю).
Но набор a1… an выбран так, что правые части равны, следовательно, g(0)=g(1), и константа получена. •
Примеры. Рассмотрим функцию f(y,z) = y ↓ z. Она несамодвойственна, так как на противоположных наборах 01 и 10 принимает одно и то же значение 0. В качестве набора a1a2 возьмем набор 01. Положим y=x0=x и z=x1=x, получим
Аналогично, рассмотрев функцию h(y,z)=y/z, которая на тех же противоположных наборах принимает значение 1, получим: