xz yz)
равна 2. Из элементарных булевых функций линейными
являются, например, инверсия
и эквивалентность. Не являются линейными,
например, штрих Шеффера и стрелка Пирса.
•Определение. Булева функция называется линейной (принадлежит классу L), если ее полином Жегалкина линеен.
Примеры.
Мажоритарная функция не является линейной:
степень ее
полинома Жегалкина (xy xz yz)
равна 2. Из элементарных булевых функций линейными
являются, например, инверсия
и эквивалентность. Не являются линейными,
например, штрих Шеффера и стрелка Пирса.
•
Утверждение о числе булевых функций класса L. Число различных линейных булевых функций, зависящих от n переменных, равно 2n+1.
Доказательство. Полином Жегалкина линейной функции f(x1, …, xn) имеет вид:
a1x1 a2x2 … an xn,где a0, …, an – булевы константы. Таким образом, каждый линейный полином определяется булевым вектором a0… an длины n+1, и наоборот, каждый булев вектор длины n+1 задает линейный полином Жегалкина некоторой функции n аргументов. Следовательно, число линейных полиномов (а значит, и число различных линейных функций n аргументов) равно числу булевых векторов длины n+1, то есть равно 2n+1. •
Пример. Из всех 16 булевых функций двух аргументов
x1, x2
8 функций (22+1) принадлежат классу L: 0, 1,
, 
, тождественные функции x1 и x2
и их инверсии x 1 и x 2. •
Теорема о замкнутости класса L. Множество всех линейных булевых функций является замкнутым классом.
Доказательство. Рассмотрим суперпозицию любых булевых функций из L, то есть функцию
и покажем, что она является линейной. Представим каждую из функций, образующих суперпозицию, полиномом Жегалкина:
α1y1 …
αm ym,
β11 x1 …
βn1 xn,·
β1m x1 …
βnm xn.Подставив эти полиномы в суперпозицию, получим:
α1(f1(x1, …, xn) … αm fm(x1, …, xn)
= α1(β01 β11 x1 … βn1 xn)
…
αm(β0m β1m x1 … βnm xn)= α1β01 …
αm β0m) (α1β11 … αm β1m)x1…
(α1βn1 … αm βnm)xn.
Поскольку в последней формуле каждая скобка есть булева константа, то получен линейный полином Жегалкина. Значит, функция f(x1, …, xn) линейная, и класс L замкнут. •
Лемма о нелинейной булевой функции. Если булева функция нелинейная, то из нее подстановкой вместо аргументов констант, переменных x, y, их инверсий x , y и, возможно, инверсией самой функции можно получить конъюнкцию xy.
Доказательство. Рассмотрим полином Жегалкина нелинейной функции f(x1, …, xn). Выберем в нем конъюнкцию K ранга больше единицы (такая конъюнкция существует, так как функция нелинейна). Не умаляя общности, можно считать, что K содержит переменные x1 x2 . Разобьем множество конъюнкций полинома на четыре группы: – первую образуем из конъюнкций, содержащих x1 и x2, – вторую – из конъюнкций, содержащих x1 и не содержащих x2, – третью – из конъюнкций, содержащих x2 и не содержащих x1 – остальные конъюнкции отнесем к четвертой группе.
В первых трех группах вынесем за скобки соответственно x1x2, x1 и x2 :
x1q(x3, …, xn)
x2 r(x3, …, xn) s(x3, …, xn).
Первая группа не пуста, так как есть по крайней мере одна конъюнкция K, содержащая x1 и x2 . Значит, найдется набор a3 … an такой, что p(a3, …, an) = 1. Подставим его в функцию f(x1, …, xn) (подстановка констант допустима по условию теоремы):
x1q(a3, …, an)
x2 r(a3, …, an)
s(a3, …, an) =
x1x2 x1a x2 b c,где a, b, c – булевы константы.
Если a=b=c=0, конъюнкция получена. Иначе положим
в последней формуле
x1= x b, и x2 = y a
(подстановка переменных x, y и их инверсий
x 1, y 1 допустима по условию
теоремы), раскроем скобки и удалим пары одинаковых конъюнкций:
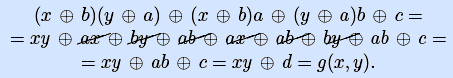
Если булева константа d=0, конъюнкция xy получена. Иначе функция g(x,y)=x y. Тогда, инвертировав исходную функцию (что допустимо по условию теоремы), получим конъюнкцию xy. •
Пример. Рассмотрим нелинейную булеву функцию, заданную полиномом Жегалкина.
x1x4
x1x2 x3x2 x4 x1x3 x3x4
1=
[ выберем первую конъюнкцию x1x2 x3x4, в ней выберем переменные x1, x2 и сгруппируем конъюнкции ]
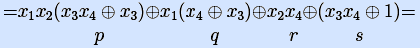
[ p(x3,x4)=1 при x3=1, x4=0, подставим эти значения переменных в формулу ]
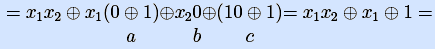
[ положим x1=x b = x, x2 =y a=y 1 ]
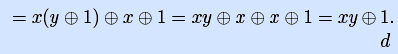
Инвертировав исходную функцию, получим конъюнкцию xy. •