15.1. Класс булевых функций, сохраняющих константу 0

Определение. Булева функция сохраняет константу 0 (принадлежит классу T0), если на наборе из всех нулей функция принимает значение ноль.

Примеры. Мажоритарная булева функция сохраняет константу 0 (принадлежит классу T0):

Из элементарных булевых функций классу T0 принадлежат, например, конъюнкция и тождественная функция; не принадлежат классу T0, например, штрих Шеффера и стрелка Пирса. •

Утверждение о числе булевых функций класса T0. Число различных булевых функций, зависящих от n переменных и сохраняющих константу 0, равно 22n –1.

Доказательство. Число различных булевых функций n аргументов равно 22n (по теореме о числе булевых функций). В векторном представлении булевых функций первая компонента задает значение функции на наборе из всех нулей. Ровно половина из 22n векторов содержит в первой компоненте ноль, поэтому число функций, сохраняющих константу 0, есть 22n/2=22n –1. •

Пример. Из всех 16 булевых функций двух аргументов x1, x2 8 функций (222 –1) принадлежат классу T0: 0, 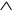, , , , 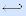и тождественные функции x1 и x2 . •

Теорема о замкнутости класса T0. Множество всех булевых функций, сохраняющих константу 0, является замкнутым классом.

Доказательство. Рассмотрим суперпозицию любых булевых функций из T0, то есть функцию

f(x1, …, xn)= f0(f1(x1, …, xn), …, fm(x1, …, xn)),

и покажем, что на наборе из всех нулей суперпозиция принимает значение ноль.

f(0, …, 0)= f0(f1(0, …, 0), …, fm(0, …, 0))=

[ учтем, что f1(x1, …, xn) T0, …, fm(x1, …, xn) T0 ]

=f0(0, …, 0) = [ учтем, что f0(y1, …, ym) T0 ] =0.

Из этого следует, что суперпозиция f(x1, …, xn) принадлежит классу T0, значит, класс T0 замкнут. •

Лемма о булевой функции, не сохраняющей константу 0. Если булева функция не сохраняет константу 0, то из нее подстановкой вместо каждого аргумента переменной x можно получить либо константу 1, либо инверсию x .

Доказательство. Рассмотрим булеву функцию f(x1, …, xn), не сохраняющую константу 0. Заменив каждый ее аргумент xi на x (такая подстановка допустима по условию леммы), получим функцию одного аргумента g(x) = f(x, …, x). Исследуем ее.

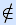g(0)=f(0, …, 0) = 1, так как f(x1, …, xn) T0.

Если g(1)=1, то g(x) – константа 1. Если g(1)=0, то g(x)=x . •

Примеры. Рассмотрим две функции, не сохраняющие константу 0: стрелку Пирса a↓ b и импликацию a b. Подставляя в них вместо аргументов переменную x, получаем:

x ↓ x = x , x x = 1.•