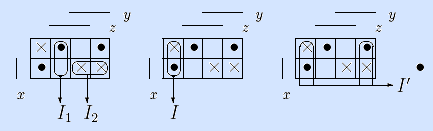 M1f, M0
M1f, M0  M0f.
M0f.Определение. Назовем доопределением неполностью определенной булевой функции f×(x1, …, xn) любую булеву функцию f(x1, …, xn), удовлетворяющую условиям:
M1f×  M1f, M0
M1f, M0  M0f.
M0f.
Это означает, что значения любого доопределения должны совпадать со значениями функции f×(x1, …, xn) на наборах из множеств M1f× и M0f×, и доопределение может принимать любые значения на наборах из M×f×. Из этого и из теоремы о числе векторов с очевидностью следует утверждение.
Утверждение о числе доопределений. Число различных доопределений неполностью определенной булевой функции f×(x1, …, xn) равно 2k, где k=|M×f×|.
Пример. Рассмотренная в предыдущем примере неполностью определенная булева функция имеет восемь доопределений.
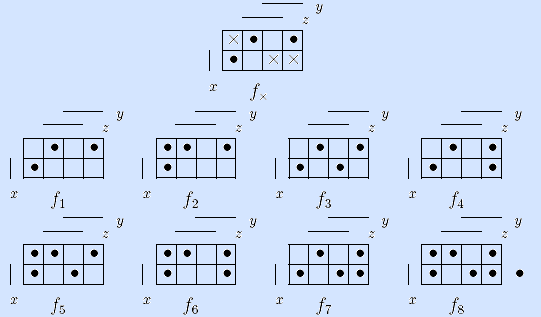
Определение. Минимизировать неполностью определенную булеву функцию – это значит выбрать среди кратчайших ДНФ всех ее доопределений самую короткую ДНФ.
Пример. Для рассмотренной в предыдущем примере функции f×(x,y,z) самой короткой оказывается кратчайшая ДНФ доопределения f6(x,y,z).

Таким образом, тот факт, что неполностью определенная булева функция задается не на всем булевом пространстве, а лишь на его подмножестве, мы используем для такого ''выгодного'' доопределения функции, которое приводит к наиболее короткой ДНФ и (согласно рассуждениям из раздела 11) к наиболее простой схеме, реализующей функцию.
Конечно, как и в случае полностью определенной булевой функции, возможны другие постановки задачи минимизации неполностью определенной функции – например, найти ее приближенную кратчайшую ДНФ.
Определение. Интервал I назовем допустимым для неполностью определенной булевой функции f×(x1, …, xn), если он удовлетворяет условиям: 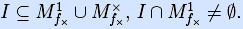
Определение. Интервал I назовем максимальным для неполностью
определенной булевой функции, если он допустим для этой
функции,
и не существует другого допустимого для нее интервала I' такого, что I 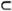 I'.
I'.
Пример. На левой матрице Грея изображены два недопустимых интервала I1= – 0 1 и I2= 0 1 – , на средней – допустимый интервал I= – 0 0 (но не максимальный), на правой – максимальный I'= – – 0.