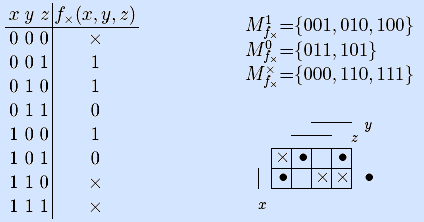B, M
B, M 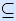 Bn.
Bn.Определение. Неполностью определенной (частичной)
булевой функцией
f×(x1, …, xn) назовем однозначное отображение подмножества
M булева пространства
Bn в булево множество B, т.е.
f : M  B, M
B, M 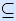 Bn.
Bn.
Как видно из определения, частным случаем неполностью определенной булевой функции является булева функция: ее областью определения является все булево пространство. Булеву функцию также можно называть полностью определенной булевой функцией.
Неполностью определенная булева функция может быть задана различными способами, аналогичными способам задания булевой функции, в частности, таблицей истинности, матрицей Грея и характеристическими множествами.
1) Задание частичной булевой функции таблицей истинности. В левой части таблицы истинности представляются, как и раньше, все векторы булева пространства, а в ее правой части либо перечисляются значения функции, либо указывается специальный символ × (если набор в область определения не входит).
2) Задание частичной булевой функции характеристическими множествами. К двум известным нам характеристическим множествам M1f× и M0f× добавляется третье, M×f×, состоящее из наборов, на которых функция не определена (для задания функции достаточно указать любые два из трех множеств).
3) Задание частичной булевой функции матрицей Грея. В матрице Грея тем же символом × отмечаются клетки, не входящие в область определения.
Пример. Пусть функция f×(x, y, z) задана на множестве булевых векторов, представляющих целые числа от 1 до 5, и принимает значение 1, если и только если заданное число есть 2k, где k – целое. Ее таблица истинности, характеристические множества и матрица Грея имеют вид: