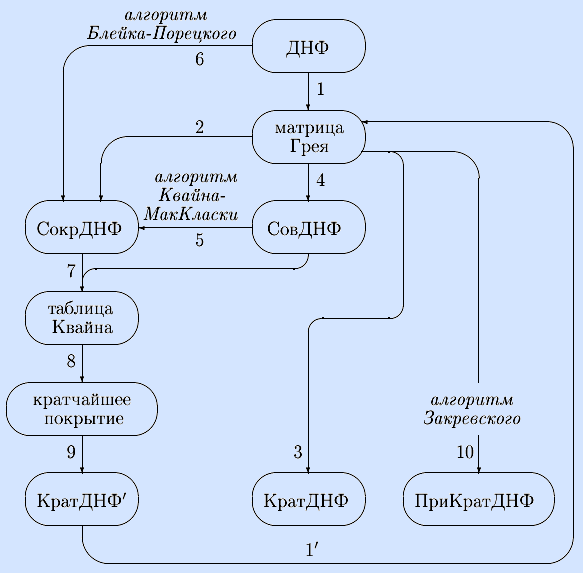
Тема контрольной работы: минимизация булевых функций.
Схема контрольной работы (решение каждой из 11 задач начинать с постановки задачи и делать выводы из сравнения полученных разными способами сокращенных ДНФ, матриц Грея, кратчайших и приближенной кратчайшей ДНФ).
1) a b c d 
a b c
a b d a c d
a b c d b c d
a b c d
2) a b c a c d
b c d a b c d
a c d a b c d
a b c d
3) a b c d
a c d
a c d
a b d a b c d
a b c d
a b c
4) a b c d a b c
a c d a b c d
a b c a c d
a b c d
5) a c d a c d
b c d a b c d
a b c d a b c d
b c d
6) a b c d
a b c d
a b c d a b d
a b c a c d
a c d.
7) a c d a b d
a c d a b c d
a b c d
a b c d
a b c
8) a b c a b c d
a b c a b c d
a c d a b c d
a c d
9) a c d
a b c d
a c d a b d
a b c d a b c d
a b d
10) a b c d a b c
b c d b c d
a b d a b c d
a b c d
11) a c d a b c d
a b c b c d
a b d a b c d
a b c d
12) a b c a c d
a b c d a b c d
a b c d
a b c
a c d
13) a b c a c d
b c d a b c
a b c d
a b c d
a b c d
14) a c d a b c
a b c a b c d
a c d a b c d
a b c d
15) a c d a c d
a b c d
a b c d
a b c a b c
a b d
16) b c d a b c d
a b d a c d
a b c a b c d
b c d
17) a c d b c d
a b c a b d
a b c d
a b c d
a b c d
18) a c d a b c
a c d a b c d
a b c a b c d
a b c d
19) a b c
a b c d
a c d a b c
a b c d
a b d
a c d
20) a c d a b d
b c d a b c
a b c d a b c d
a b c d
21) a b c d a b c d
a b c c d
a b c a b c d
a c d
22) a b d a b c
a b d b c d
a b c d a b c d
a b c d
23) a c d a b d
a b c d a b c
b c d a b c
a b c d
24) b c d a b d
a b d a b c
a b c d
a b c d a b c d
25) b c d
a b c d
a b d a b c d
a b c a c d
a b c d
26) a b d a b c d
a c d a b c d
a c d a b d
a b c d
27) a c d a b c
a b c a b c d
a b c d a c d
a b c d
28) a c d a b c d
a b c d a c d
a b c a b c d
b c d
29) a b c d a c d
a b d a b c d
a c d a b c
a b c d
30) a b d a b c
a c d a b c d
a b d a b
a b c d
Пример. Задана ДНФ булевой функции.
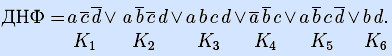
1) Построим матрицу Грея функции по заданной ДНФ.
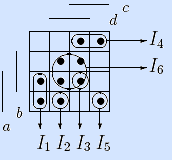
2, 3) Найдем сокращенную и кратчайшую ДНФ по матрице Грея. Все максимальные интервалы A –E (левая и средняя матрицы) задают сокращенную ДНФ. Достаточное множество из минимального числа максимальных интервалов (правая матрица) задает кратчайшую ДНФ.
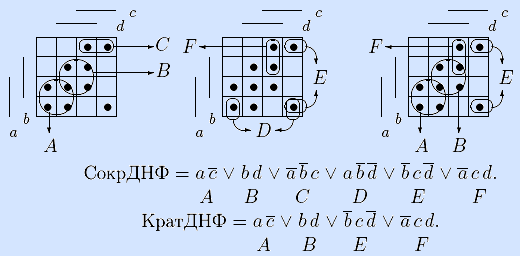
4) Построим совершенную ДНФ функции по матрице Грея. Каждая точка задает конъюнкцию совершенной ДНФ.
a b cd
a bc d
a bcd
abc d
abc d
abcd
ab c d ab c d
ab cd . 5) Построим сокращенную ДНФ функции из совершенной ДНФ алгоритмом Квайна-МакКласки. Представляем совершенную ДНФ списком точек, упорядочиваем их по весу и разбиваем на классы.
Выполняем все неполные склеивания векторов классов Ci и Ci+1, i =1,2,3, отмечая участников склеивания. Результаты заносим в список 1 (с номерами склеиваемых векторов). Повторяя аналогичные действия для списка 1, получаем список 2 и приводим в нем подобные. Склеивание векторов из списка 2 невозможно.
Неотмеченные векторы всех списков задают сокращенную ДНФ (обозначения конъюнкций взяты из задачи 2).
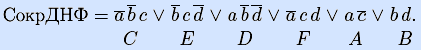
6) Построим сокращенную ДНФ функции из исходной ДНФ алгоритмом Блейка-Порецкого. Представляем ДНФ списком троичных векторов, удаляем третий вектор, как поглощаемый шестым. Затем, обобщенно склеивая каждый очередной вектор со всеми предыдущими, получаем, как видно из списка, векторы с седьмого по пятнадцатый. Они либо поглощаются предыдущими, либо остаются в списке, поглощая некоторые из предыдущих векторов.
Решение образуют шесть непоглощенных векторов, они задают сокращенную ДНФ (обозначения конъюнкций взяты из задачи 2).
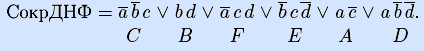
Вывод. Сокращенные ДНФ, полученные в задачах 2), 5), 6), совпадают, следовательно, они найдены верно.
7) Построим таблицу Квайна функции по ее совершенной и сокращенной ДНФ. На левой матрице нумеруем точки, на остальных повторяем все максимальные интервалы из задачи 2).
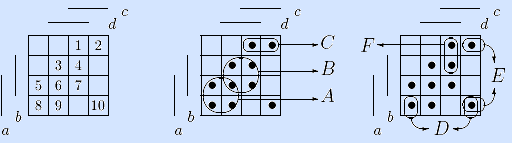
Проверяя принадлежность точек максимальным интервалам, строим таблицу Квайна:
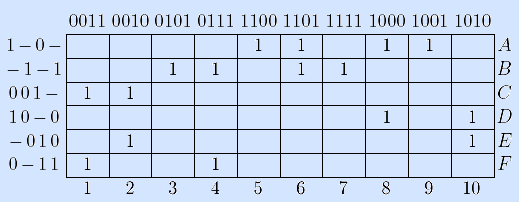
8) Найдем кратчайшее покрытие таблицы Квайна. В ней нет однострочного покрытия, но
строки A и B – ядерные, включаем их в покрытие и
вычеркиваем из матрицы вместе с покрытыми столбцами (с третьего по девятый), получаем матрицу Q1.
В ней нет однострочных покрытий и ядерных столбцов, но есть
строка-предшественница:
D 
E, поэтому удаляем строку D. В новой матрице Q2
появилась ядерная строка E, включаем ее в покрытие и удаляем из матрицы вместе со вторым
и десятым столбцами, получаем матрицу Q3.
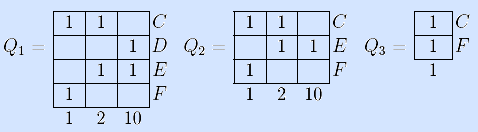
Строка C образует однострочное покрытие матрицы Q3. Включив ее в решение, получаем кратчайшее покрытие {A,B,C,E}.
9) Запишем кратчайшую ДНФ по кратчайшему покрытию таблицы Квайна.
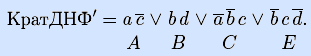
1') Построим матрицу Грея по полученной кратчайшей ДНФ.
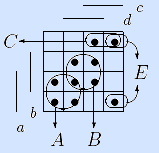
Вывод. Матрицы Грея, из задач 1) и 1') совпали, значит, кратчайшая ДНФ из задачи 9) задает исходную функцию. Кроме того, длины кратчайших ДНФ из задач 3) и 9) равны, значит, эти задачи решены верно.
10) Построим приближенную кратчайшую ДНФ по матрице Грея алгоритмом Закревского. На левой матрице показываем цены точек, на правой обозначаем точки.
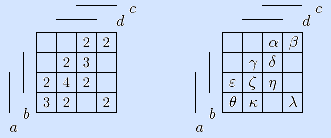
Выбираем точку α минимальной цены 2. Она входит в два максимальных интервала (левая матрица внизу). Оба интервала содержат по две неотмеченных точки, и оба одинаковой мощности, поэтому в решение включаем любой из них. Отмечаем точки (на средней матрице).
Выбираем неотмеченную точку γ минимальной цены 2. Она входит в один максимальный интервал (средняя матрица), включаем его в решение и отмечаем точки (на правой матрице).
Выбираем неотмеченную точку ε минимальной цены 2. Она входит в один максимальный интервал (правая матрица), включаем его в решение и отмечаем точки (на следующей матрице).
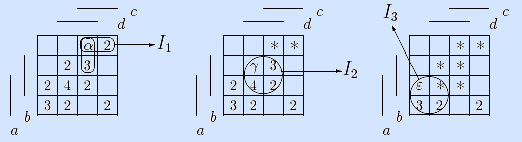
Выбираем неотмеченную точку λ минимальной цены 2. Она входит в два максимальных интервала. Оба содержат по одной неотмеченной точке, и оба одинаковой мощности, поэтому в решение включаем любой из них и отмечаем его точки.
Поскольку все точки отмечены, идем на конец.
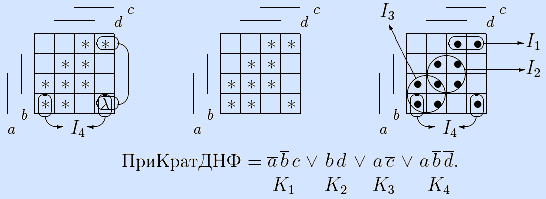
Вывод. Так как приближенная кратчайшая ДНФ задает исходную функцию, и ее длина не меньше длин кратчайших ДНФ из задач 3) и 9), то приближенная кратчайшая ДНФ найдена верно. •