Остановимся лишь на одном из методов поиска приближенных кратчайших ДНФ. Как показало его тестирование на функциях небольшого числа аргументов, метод находит чаще всего либо кратчайшую ДНФ, либо отличающуюся от кратчайшей только на одну конъюнкцию.
Алгоритм Закревского (ориентирован на матричное представление функции и визуальный способ решения).
Начало. Задана матрица Грея булевой функции.
Шаг 1. Для каждой точки вычислим цену – количество соседних ей точек. Все точки будем считать неотмеченными.
Шаг 2. Среди неотмеченных точек рассмотрим точку минимальной цены и найдем все содержащие ее максимальные интервалы. Выберем из них тот, который содержит наибольшее число неотмеченных точек. Если таких интервалов несколько, то выберем из них интервал наибольшей мощности.
Шаг 3. Включим выбранный интервал в решение и отметим на матрице его точки. Если не все точки отмечены, то идем на шаг 2.
Конец. Включенные в решение интервалы задают приближенную кратчайшую ДНФ.
Пример. Рассмотрим матрицу Грея функции из последнего примера.
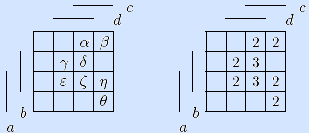
Начало. Точки обозначаем греческими буквами (левая матрица).
Шаг 1. Вычисляем цены точек (правая матрица).

Шаги 2, 3. Выбираем точку α (минимальной цены 2). Она входит в два максимальных интервала (левая матрица). Оба интервала содержат по две неотмеченные точки и имеют одинаковые мощности, поэтому включаем в решение любой из них и отмечаем его точки (правая матрица).
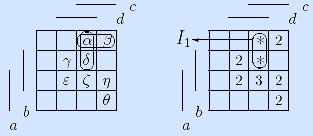
Поскольку не все точки отмечены, идем на шаг 2.
Шаги 2, 3. Выбираем неотмеченную точку β (цены 2). Она входит в два максимальных интервала (с одной и двумя неотмеченными точками), поэтому включаем в решение интервал I2 с двумя неотмеченными точками и отмечаем их.
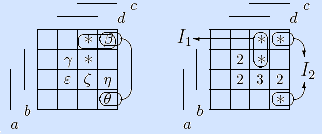
Поскольку не все точки отмечены, идем на шаг 2.
Шаги 2, 3. Выбираем неотмеченную точку γ (цены 2). Она входит в один максимальный интервал, включаем его в решение и отмечаем точки.
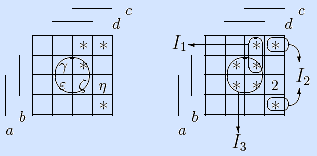
Поскольку не все точки отмечены, идем на шаг 2.
Шаги 2, 3. Выбираем неотмеченную точку η (цены 2). Она входит в два максимальных интервала, содержащих по одной неотмеченной точке. Мощности интервалов равны, поэтому включаем в решение любой интервал и отмечаем его точки. Поскольку все точки функции отмечены, идем на конец.
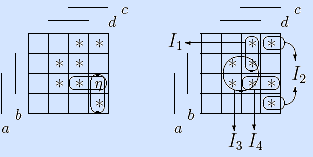
Конец.
ПриКратДНФ =
a c d  b c d
b c d  b d
b d  a b c.
a b c.
Полученная ДНФ не является кратчайшей для рассмотренной функции (см. 11.3), но кратчайшая ДНФ могла быть получена данным алгоритмом, если бы при первом выполнении шага 2 вместо I1 в решение был включен другой максимальный интервал (проверьте эту возможность самостоятельно).
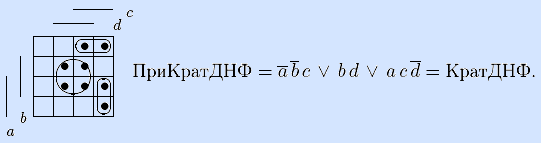
Рассмотренный пример еще раз подчеркивает приближенный характер алгоритма Закревского. Поэтому при его использовании стоит проверить полученную ДНФ на безызбыточность. •