11.2.3. Поиск всех безызбыточных покрытий

Очевидно, что все кратчайшие и минимальные покрытия матрицы безызбыточны. Поэтому поиск всех таких покрытий можно свести к построению всех безызбыточных покрытий и выделению из них кратчайших и минимальных. Тривиальный метод поиска всех безызбыточных покрытий состоит в переборе и анализе всех подмножеств строк матрицы. Однако, число перебираемых подмножеств велико (2^m, где m – число строк матрицы), поэтому остановимся на другом, более эффективном методе.

Будем предполагать, что матрица имеет покрытие, то есть не содержит столбцов, целиком состоящих из нулей (для таблицы Квайна это условие всегда выполняется), и прежде всего попытаемся упростить матрицу.

Определение. Столбец булевой матрицы назовем ядерным, если он содержит ровно одну единицу. Строку булевой матрицы назовем ядерной, если она покрывает ядерный столбец.

Пример. В матрице Q ядерными являются столбцы 1, 4 и строки A, B. •

Очевидно, что ядерные строки входят в любое покрытие, что дает возможность сформулировать следующее правило упрощения матрицы.

Правило ядерной строки. Если в матрице есть ядерная строка, то она включается в любое искомое покрытие и удаляется из матрицы вместе со всеми столбцами, которые ядерная строка покрывает. Удаляются также пустые строки (состоящие из нулей), которые при этом могут появиться.

Пример. Применим правило ядерной строки дважды к знакомой нам матрице Q. В результате строки A и B будут включены в покрытие, а матрица упростится.

В частности, если все столбцы матрицы покрываются ядерными строками, то эти строки образуют единственное ее безызбыточное покрытие.

Упростив булеву матрицу по правилу ядерной строки, и оставив в ней по одному из одинаковых столбцов (что, очевидно, не повлияет на решение), продолжим поиск всех безызбыточных покрытий упрощенной матрицы.

Припишем ее строкам булевы переменные s₁ …, s_m, обозначим через S произвольное подмножество строк и положим s_i = 1, если и только если i-я строка принадлежит множеству S, то есть будем задавать подмножество S строк матрицы набором значений переменных s₁ …, s_m.

Определение. Булеву функцию p(s₁, …, s_m), принимающую значение единицы на тех и только тех наборах σ, которые задают покрытия матрицы, назовем функцией покрытия матрицы.

Пример. Зададим формулой функцию покрытия предыдущей матрицы Q', исходя из следующих рассуждений.

Первый столбец покрывается подмножеством строк S, если и только если в S входят:

– либо строка C (переменная C=1),

– либо строка F (переменная F=1),

– либо обе строки одновременно (C=1 и F=1),

то есть если и только если C F=1.

Аналогично второй столбец покрывается подмножеством S, если и только если C H=1, и так далее для всех столбцов.

Все столбцы покрываются подмножеством строк S, то есть p(σ)=1, если и только если одновременно выполняются все перечисленные условия, то есть (C F)(C H)… =1. Это означает, что функцию покрытия матрицы Q' можно задать формулой:

p(C, …, H) = (C F)(C H)(E F) (D H)(D G)(E G).

В общем случае для матрицы с k столбцами функция покрытия задается конъюнкцией вида D₁ ·… · D_k, где D_j – дизъюнкция всех переменных, приписанных строкам с единицей в j-м столбце. Будем называть полученную формулу конъюнктивной нормальной формой (КНФ) функции покрытия:

p(s₁, …, s_m) = D₁ ·… · D_k = КНФ_p.

Так как каждое слагаемое дизъюнкции D_j задает безызбыточное покрытие j-го столбца, то, перемножив дизъюнкции D_i и D_j, мы получим все безызбыточные покрытия столбцов i и j (но не только безызбыточные).

Пример. Перемножим первые две дизъюнкции предыдущего примера:

(C F)(C H) = C CH CF FH.

Получены не только все безызбыточные покрытия первых двух столбцов: {C} и {F,H}, но и покрытия {C,H} и {C,F}, которые содержат строку C, поэтому не являются безызбыточными (это эквивалентно тому, что конъюнкции CH и CF поглощаются конъюнкцией C). •

Обобщая приведенные рассуждения на все столбцы булевой матрицы, приходим к выводу, что для построения всех безызбыточных покрытий матрицы надо перемножать все дизъюнкции КНФ функции покрытия, выполняя при этом все возможные поглощения. В результате будет получена ДНФ, конъюнкции которой зададут все безызбыточные покрытия.

Алгоритм поиска всех безызбыточных покрытий булевой матрицы (основан на построении КНФ функции покрытия и преобразовании ее в ДНФ с выполнением поглощений).

Начало. Задана булева матрица.

Шаг 1. Применим к матрице правило ядерной строки многократно, пока это возможно. Если матрица стала пустой, то идем на конец. Иначе из равных столбцов оставим по одному, пронумеруем столбцы упрощенной матрицы и припишем строкам булевы переменные s₁ …, s_m.

Шаг 2. Выберем очередной (j-й) столбец матрицы. Если столбцы исчерпаны, идем на шаг 3. Иначе построим дизъюнкцию D_j переменных, приписанных строкам, покрывающим j-й столбец, и идем на шаг 2.

Шаг 3. Из полученных дизъюнкций построим конъюнктивную нормальную форму D₁ ·… · D_k.

Шаг 4. Раскроем скобки в КНФ, выполняя поглощения конъюнкций. Получим ДНФ=K₁… K_t.

Конец. Конъюнкции K₁, …, K_t задают все безызбыточные покрытия упрощенной матрицы. Добавив к каждому из них ядерные строки (выделенные на первом шаге), получим все безызбыточные покрытия исходной матрицы.

Пример. Продемонстрируем алгоритм на знакомой нам булевой матрице Q. Для нее уже выполнен шаг 1: строки A и B выделены как ядерные и удалены вместе с первыми четырьмя столбцами. В результате получена упрощенная матрица и построена КНФ функции ее покрытия (шаг 2 повторен 6 раз и выполнен шаг 3):

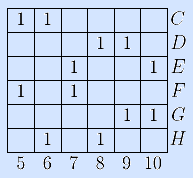
КНФ= (C F)(C H)(E F) (D H)(D G)(E G).

Шаг 4. Перемножив скобки в КНФ (удобнее перемножать первую на вторую, третью на шестую и четвертую на пятую скобки) и выполнив поглощения, получим ДНФ.

(C F H) (E F G) (D G H) =(C E C F G E F H F G H) (D G H)=

= C D E C E G H C D F G C F G H

D E F H E F G H D F G H F G H =

= C D E C E G H C D F G D E F H F G H = ДНФ.

Конец. Конъюнкции ДНФ задают все безызбыточные покрытия упрощенной матрицы:

Добавив к каждому из них ядерные строки A и B, выделенные на первом шаге, получим все безызбыточные покрытия исходной матрицы (два покрытия длины 5 и три покрытия длины 6):