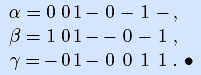11.1. Получение сокращенной ДНФ – первый этап минимизации

Изучим два метода получения сокращенной ДНФ, но прежде вспомним законы поглощения и склеивания конъюнкций и добавим к ним закон неполного склеивания.

Закон поглощения: K₁ K₁K₂= K₁.

Закон склеивания: x K x K = K.

Закон неполного склеивания: x K x K = x K x K K.

Закон обобщенного склеивания: x K₁ x K₂= x K₁ x K₂ K₁K₂.

Очевидно, что закон неполного склеивания следует из закона обобщенного склеивания (при K₁=K₂=K), а закон склеивания – из закона неполного склеивания (если в последнем выполнить поглощения конъюнкций).

Переведем эти законы на язык интервалов, используя интервалы и представляющие их троичные векторы как синонимы.

Закон поглощения говорит о том, что если объединение двух интервалов I и I' совпадает с I, то интервал I' содержится в интервале I (поглощается им). Значит, поглощаемый вектор должен получаться из поглощающего заменой некоторых его внутренних компонент ( –) на внешние (0 или 1).

Пример. В паре троичных векторов 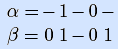вектор β поглощается вектором α. •

Закон склеивания объединяет два соседних интервала в один. Напомним, что соседние интервалы совпадают по номерам внешних компонент, но различаются по значению ровно одной из них (ортогональной). При склеивании получается интервал, который отличается от исходных лишь в ортогональной компоненте – она становится внутренней (операция склеивания соседних интервалов уже рассматривалась в подразделе 2.2.3).

Пример. Результатом склеивания соседних векторов α и β является вектор γ:

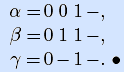
Закон неполного склеивания объединяет два соседних интервала и добавляет к результату исходные интервалы.

Пример. Результатом неполного склеивания векторов α и β из предыдущего примера являются три вектора: α, β и γ. •

Закон обобщенного склеивания объединяет соседние части двух смежных интервалов. Смежные интервалы могут не совпадать по номерам внешних компонент, но должны быть ортогональны ровно по одной из них. Результатом обобщенного склеивания являются три интервала: два исходных и третий, который строится следующим образом:

– компоненты, по которым исходные векторы совпадают, сохраняют свои значения;

– компоненты, которые в одном из векторов являются внешними, а в другом – внутренними, принимают значения внешних компонент;

– ортогональная компонента становится внутренней.

Пример. Результатом обобщенного склеивания смежных векторов α и β являются векторы α, β и γ: