15.5. Класс монотонных булевых функций

Определение. Булева функция f(x₁, …, x_n) называется монотонной (принадлежит классу M), если для любой пары наборов α и β таких, что αβ, выполняется условие f(α)≤ f(β) (назовем его условием монотонности).

Примеры. Исследуем мажоритарную булеву функцию.

Перебор пар начнем с наборов α=000 и β=001: для них αβ и выполнено условие монотонности f(000)=f(001). Отметим, что набор α таков, что любой другой набор β является последователем α, и, казалось бы, следует анализировать каждую из этих пар. Однако f(α)=0, поэтому условие f(α)≤ f(β) будет выполнено для любого набора β. Значит, в качестве α достаточно рассмотреть лишь те наборы, на которых функция принимает значение единица: 011, 101, 110 и 111. Кроме того, наборы в таблице истинности расположены в естественном порядке, значит, наборы –последователи лежат ниже предшественников. Набор α=011 имеет единственного последователя β=111 и f(011)=f(111), то есть условие монотонности для этой пары не нарушено. Рассмотрим остальные возможные пары наборов: α=101, β=111 и α=110, β=111 (набор α=111 последователей не имеет). Для них условие монотонности также не нарушено. Значит, мажоритарная функция монотонна.

Из элементарных булевых функций монотонными являются, например, конъюнкция и дизъюнкция. Не являются монотонными, например, штрих Шеффера и стрелка Пирса. •

В общем случае набор имеет несколько последователей, и для всех таких пар надо проверять выполнение условия монотонности. Чтобы сформулировать более простой алгоритм распознавания монотонной функции, докажем утверждение, которое к тому же будет использовано при доказательстве леммы о немонотонной функции.

Утверждение о условии немонотонности. Для любой пары наборов α и β таких, что αβ и f(α) > f(β), найдется пара соседних наборов α', β' с теми же свойствами: α'β' и f(α') > f(β').

Доказательство. Если α и β – соседи, то утверждение верно (α'=α, β'=β). Иначе вычислим расстояние d (по Хэммингу) между наборами α=a₁… a_n и β=b₁… b_n и начнем строить цепочку наборов γ₀, …, γ_d такую, что

α=γ₀γ₁… γ_{d –1}γ_d=β,

и любые два расположенных рядом набора γ_{i –1},γ_i (i=1, …, d) являются соседями. Очередной набор γ_i получим из предыдущего набора γ_{i –1} заменой значения одной из ортогональных компонент наборов γ_{i –1} и β (это будет замена 0 на 1, так как αβ), затем проверим условие немонотонности f(γ_{i –1})>f(γ_i). Если оно выполнено, утверждение доказано (α'=γ_{i –1}, β'=γ_i). Иначе получим и исследуем очередной набор. В худшем случае, когда постоянно выполняется условие монотонности, имеем

но тогда f(γ_{d –1})=1 и f(β)=0, значит, условие немонотонности выполнится для последней пары: α'=γ_{d –1} и β'=γ_d=β. •

Пример. Пусть задана пара булевых векторов , тогда цепочка соседей может иметь следующий вид:

Если f(α)>f(β), то смена значения функции с 1 на 0 произойдет по крайней мере на одной из четырех пар соседей. •

Алгоритм распознавания монотонной булевой функции (основан на утверждении о условии немонотонности).

Начало. Задана таблица истинности булевой функции.

Шаг 1. Сравниваем значения функции на наборах, соседних по первой переменной, то есть верхнюю половину столбца значений функции (вектор φ₁) с нижней половиной (вектор φ₁). Если условие φ₁φ₁ нарушено, то функция не монотонна, идем на конец.

Шаг 2. Сравниваем значения функции на наборах, соседних по второй переменной, то есть верхние четвертины столбца значений функции (векторы φ'₂, φ''₂) с нижними четвертинами (векторами φ'₂, φ''₂) в каждой половине. Если хотя бы одно из условий φ'₂φ'₂ и φ''₂φ''₂нарушено, то функция не монотонна, идем на конец.

Шаги 3 –n. Аналогично сравниваем восьмые, шестнадцатые части, и так далее. Если ни одно из проверяемых условий не нарушено, то функция монотонна.

Конец.

Примеры. Рассмотрим две булевых функции (первая – мажоритарная).

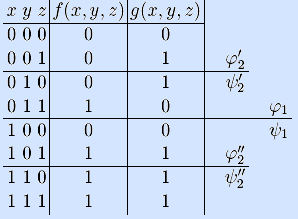
Проверим на монотонность мажоритарную функцию. Сравниваем половины столбца значений: φ₁=0001 0111=φ₁. Сравниваем четвертины: φ'₂=00 01=φ'₂, φ''₂=01 11=φ''₂. Сравниваем осьмушки: 0 0 , 0 1, 0 1 , 1 1 . Следовательно, мажоритарная функция монотонна.

Проверим на монотонность функцию g(x,y,z). Сравниваем половины столбца значений: φ₁=0110 0111=φ₁. Сравниваем четвертины: так как φ'₂=01 не предшествует φ'₂=10, функция g(x,y,z) не монотонна. •

Теорема о замкнутости класса M. Множество всех монотонных булевых функций является замкнутым классом.

Доказательство. Рассмотрим суперпозицию любых булевых функций из M, то есть функцию

и покажем, что она монотонна. Подставим в суперпозицию любую пару наборов α и β таких, что αβ, получим:

где γ и δ – булевы векторы. Так как αβ, и булевы функции f₁(x₁, …, x_n), …, f_m(x₁, …, x_n) монотонны, то γδ. Поскольку функция f₀(y₁, …, y_m) также монотонна, то f₀(γ)≤ f₀(δ), следовательно, f(α)≤ f(β), то есть f(x₁, …, x_n) монотонна, и класс M замкнут. •

Лемма о немонотонной булевой функции. Если булева функция немонотонна, то из нее подстановкой вместо аргументов констант 0 и 1 и переменной x можно получить инверсию переменной x .

Доказательство. Рассмотрим немонотонную функцию f(x₁, …, x_n). Согласно утверждению о условии немонотонности, существует пара соседних наборов α=a₁… a_n и β=b₁… b_n таких, что αβ и f(α) > f(β), то есть

Пусть α и β – соседи по k –й компоненте, тогда

Подставим в функцию f(x₁, …, x_n) вместо каждого аргумента x_i либо константу a_i, если i ≠ k, либо переменную x, если i = k (подстановка константы и переменной допустима по условию теоремы). В результате получим функцию одного аргумента

Покажем, что g(x)=x :

Итак, инверсия x получена. •

Она немонотонна, так как существует пара наборов α=00 и β=10 таких, что αβ и f(α)>f(β). Так как α и β – соседи по первой компоненте, то, согласно доказательству леммы, положим y=x и подставим вместо z константу 0, получим: